Question

Find the y intercept of y=3log2(x+3)-6

Answer 1

`\text{$y$-intercept$\;=\log_2 \left((27)/(64)\right) \approx -1.245$}`

Explanation:

The y-intercept is the value of y when x = 0.

Therefore, to find the y-intercept of y = 3 log₂(x + 3) - 6, substitute x = 0 into the equation and solve for y.

`\implies y=3 \log_2(0+3)-6`

`\implies y=3 \log_2(3)-6`

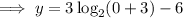
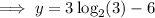
Using the log law logₐ(a) = 1, rewrite 6 with log base 2:

`\implies y=3 \log_2(3)-6\log_2(2)`

`\textsf{Apply the log power law:} \quad n\log_ax=\log_ax^n`

`\implies y=\log_2(3)^3-\log_2(2)^6`

`\implies y=\log_2(27)-\log_2(64)`

`\textsf{Apply the log quotient law:} \quad \log_ax - \log_ay=\log_a \left((x)/(y)\right)`

`\implies y=\log_2 \left((27)/(64)\right)`

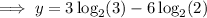
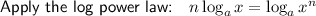
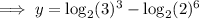
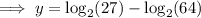
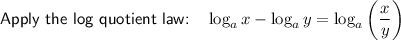
Therefore, the exact value of the y-intercept of the given equation is log₂(27/64) which is approximately -1.245 to the nearest thousandth.