Answer:
A. h'(2) = 5
B. m'(2) = -24
C. y = 8x - 31
D. j'(2) = 3/25 = 0.12
Explanation:
When differentiating composite functions, use the chain rule.
![\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\$\left[f\left(g(x)\right)\right]'=f'\left(g(x)\right) \cdot g'(x)$\\\end{minipage}}](https://img.qammunity.org/2024/formulas/mathematics/college/6zx0xt63e5myrz5yi1fwl5umk7clxfeup5.png)
Chain Rule: The derivative of a composite function is the product of the derivative of the outer function evaluated at the inner function and the derivative of the inner function.
Part A
Using the chain rule, if h(x) = g(f(x)) then h'(x) = g'(f(x)) ⋅ f'(x).
To find h'(2), substitute x = 2 into the differentiated equation:
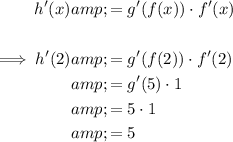
Therefore, h'(2) = 5.
Part B
Using the chain rule, if m(x) = f(x²) then m'(x) = f'(x²) ⋅ 2x.
To find m'(2), substitute x = 2 into the differentiated equation:

Therefore, m'(2) = -24.
Part C
To find the slope of the tangent line to the graph of k at x = 4, substitute x = 4 into the derivative of k(x).
If k(x) = f(g(x)) then k'(x) = f'(g(x)) ⋅ g'(x).
Therefore, the slope of the tangent line is:
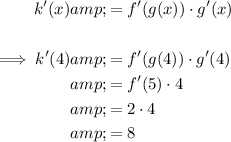
Now calculate k(x) when x = 4:
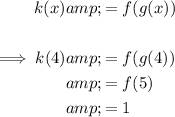
To write the equation of the tangent line, substitute the found slope m = 8 and point (4, 1) into the point-slope equation:
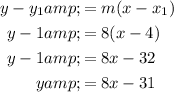
Therefore, an equation for the line tangent to the graph of k at x = 4 is:
Part D
To find the derivative of j(x) use the quotient rule.
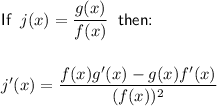
To calculate j'(2), substitute x = 2 into the equation:
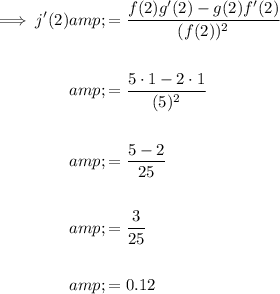
Therefore, j'(2) = 3/25 = 0.12.