Question

A Cepheid variable star is a star whose brightness alternately increases and decreases. Suppose that Cephei Joe is a star for which the interval between times of maximum brightness is 6 days. Its average brightness is 3.5 and the brightness changes by /-0.25. Using this data, we can construct a mathematical model for the brightness of Cephei Joe at time t, where t is measured in days: B(t)=4.2 +0.45sin(2pit/4.4)

A) Find the rate of change of the brightness after t days.
B) Find the rate of increase after one day.

Answer 1

a) The rate of change of the brightness after t days is
`B^(\prime)(t) = 0.204525\picos((0.4545\pi t))`

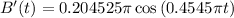
b) The rate of increase after one day is of 0.0915.

Explanation:

The brightness after t days is given by:

`B(t) = 4.2 + 0.45\sin{((2\pi t)/(4.4))} = 4.2 + 0.45sin((0.4545\pi t))`

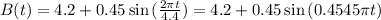
A) Find the rate of change of the brightness after t days.

This is
`B^(\prime)(t)`

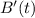
The derivative of a constant is 0, the derivative of
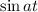`sin(at)` is
`acos(at)`

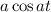
So, in this case, we have that:

`B^(\prime)(t) = 0.45*0.4545\picos((0.4545\pi t)) = 0.204525\picos((0.4545\pi t))`

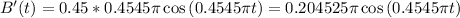
The rate of change of the brightness after t days is
`B^(\prime)(t) = 0.204525\picos((0.4545\pi t))`

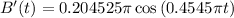
B) Find the rate of increase after one day.

This is
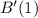`B^(\prime)(1)`. So

`B^(\prime)(1) = 0.204525\picos((0.4545\pi)) = 0.0915`

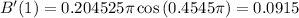
The rate of increase after one day is of 0.0915.