Question

A new process of more accurately detecting anaerobic respiration in cells is being tested. The new process is important due to its high accuracy, its lack of extensive experimentation, and the fact that it could be used to identify five different categories of organisms: obligate anaerobes, facultative anaerobes, aerotolerant, microaerophilic, and n anaerobes instead of using a single test for each category. The process claims that it can identify obligate anaerobes with 97.8% accuracy, facultative anaerobes with 98.1% accuracy, aerotolerant with 95.9% accuracy, microaerophiles with 96.5% accuracy, and n anaerobes with 99.2% accuracy. If any category is not present, the process does not signal. Samples are prepared for the calibration of the process and 31% of them contain obligate anaerobes, 27% contain facultative anaerobes, 21% contain microaerophiles, 12% contain nanaerobes, and 9% contain aerotolerant. A test sample is selected randomly.

Required:
a. What is the probability that the process will signal?
b. If the test signals, what is the probability thatmicroaerophiles are present?

Answer 1

a) 0.97605 = 97.605% probability that the process will signal.

b) 0.2076 = 20.76% probability that microaerophiles are present.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

a. What is the probability that the process will signal?

It signals in these following moments:

97.8% of 31%(contains obligate anaerobes).

98.1% of 27%(contains facultative anaerobes).

96.5% of 21%(contains microaerophiles).

99.2% of 12%(contains nanaerobes).

95.9% of 9%(contains aerotolerant). So

`p = 0.978*0.31 + 0.981*0.27 + 0.965*0.21 + 0.992*0.12 + 0.959*0.09 = 0.97605`

0.97605 = 97.605% probability that the process will signal.

b. If the test signals, what is the probability thatmicroaerophiles are present?

Event A: Test signals

Event B: Contains microaerophiles

0.97605 = 97.605% probability that the process will signal.

This means that
`P(A) = 0.97605`

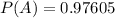
Intersection of events A and B:

Signals containing microaerophiles, which is 96.5% of 21%. So

`P(A \cap B) = 0.965*0.21 = 0.20265`

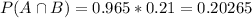
The probability that microaerophiles are present is:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.20265)/(0.97605) = 0.2076`

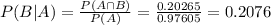
0.2076 = 20.76% probability that microaerophiles are present.