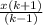Question

(Repost because urgency)

Not sure how to go about tackling this question?
Should I try to get
`y=(x(k+1))/(k-1)` into the form of the ratio by rationalizing first then simplify?

Answer 1

y =
`(x(k+1))/(k-1)`

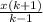
Explanation:

First, recall that in a proportion (a set of equivalent ratios), the product of means is equal to the product of extremes. For example,

if
`(a)/(b) = (c)/(d)` (or a:b = c:d) the product of means (b and c) is equal to the product of extremes (a and d), and we have ad = cb.

Using this knowledge, in the proportion (y+x):(y-x) = k:1, let us find the product of means and extremes and set them equal, like so:

(y+x):(y-x) = k:1 =

k(y-x) = y+x =

ky - kx = y+x

To solve for y, move all terms including y to one side, like so:

ky - kx = y+x =

ky - y = kx + x

Now, factor out y.

ky - y = kx + x =

y(k - 1) = kx + x

Then, factor out the common term x.

y(k - 1) = kx + x =

y(k - 1) = k(x + 1)

Now, finish isolating the variable by dividing by (k-1), and we have:

y =
`(x(k+1))/((k-1))`