Question

Answer and explain in detail​

Answer 1

The area of right-angled triangle is 30 cm².

Step-by-step Step-by-step explanation:

Given :

• Here we given that the base and hypotenuse of triangle 12 cm and 13 cm respectively.

To Find :

• We have to find the area of right-angled triangle but before we will find the height of the triangle.

Solution :

By using Pythagoras Theorem we will find the hypotenuse of triangle :

`\sf{\longrightarrow{{(Hypotenuse)}^(2) = {(Height)}^(2) + {(Base)}^(2)}}`

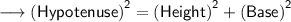
Substituting all the given values in the formula to find hypotenuse :

• Hypotenuse = 13 cm
• Base = 12 cm

`\sf{\longrightarrow{{(Hypotenuse)}^(2) = {(Height)}^(2) + {(Base)}^(2)}}`

`\sf{\longrightarrow{{(13)}^(2) = {(Height)}^(2) + {(12)}^(2)}}`

`\sf{\longrightarrow{(13 * 13) = {(Height)}^(2) + {(12 * 12)}}}`

`\sf{\longrightarrow{(169) = {(Height)}^(2) + {(144)}}}`

`\sf{\longrightarrow{{(Height)}^(2) = 169 - 144}}`

`\sf{\longrightarrow{{(Height)}^(2) = 25}}`

`\sf{\longrightarrow{{(Height)} = √(25)}}`

`\sf{\longrightarrow{\underline{\underline{\red{(Height) = 5 \: cm}}}}}`

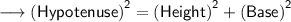
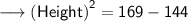
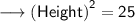
Hence, the height of triangle is 5 cm.

`\begin{gathered} \end{gathered}`

Now, calculating the area of right-angled triangle by substituting all the given values in the formula :

`\dashrightarrow{\sf{Area_((\triangle)) = (1)/(2)bh}}`

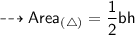
• b (Base) = 12 cm
• h (Height) = 5 cm

`\dashrightarrow{\sf{Area_((\triangle)) = (1)/(2)bh}}`

`\dashrightarrow{\sf{Area_((\triangle)) = (1)/(2) * b * h}}`

`\dashrightarrow{\sf{Area_((\triangle)) = (1)/(2) * 12* 5}}`

`\dashrightarrow{\sf{Area_((\triangle)) = 6* 5}}`

`\dashrightarrow{\sf{\underline{\underline{\pink{Area_((\triangle)) =30 \: {cm}^(2)}}}}}`

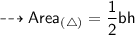
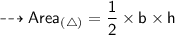
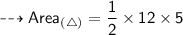
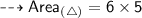
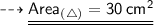
Hence, the area of triangle is 30 cm².

—————————————————