Question

Find the inverse of f(x) = (x - 5)/(x + 6)

Answer 1

`f^(-1)(x) = (6x + 5)/(1 - x)`

Explanation:

To find the inverse of a function, we can swap x and y (f(x)), then solve for y, and represent that y as
`f^(-1)(x)`.

`f(x) = (x - 5)/(x + 6)`

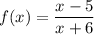
↓ swapping x and y

`x = (y - 5)/(y + 6)`

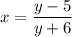
↓ multiplying both sides by (y + 6)

`x(y + 6) = y - 5`

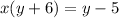
↓ simplifying using the distributive property

`xy + 6x = y - 5`

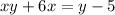
↓ subtracting 6x and y from both sides to isolate the y terms

`xy - y = - 6x - 5`

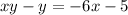
↓ undistributing y from the left side

`y(x - 1) = - 6x - 5x`

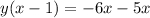
↓ dividing both sides by (x - 1)

`y = (-6x - 5)/(x-1)`

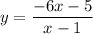
↓ (optional) multiplying the fraction by
`\bold{(-1)/(-1)}`

`y = (6x + 5)/(1 - x)`

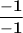
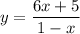
↓ replacing y with
`f^(-1)(x)`

`\boxed{f^(-1)(x) = (6x + 5)/(1 - x)}`