Question

In a Technical College, 115 students sat for Federal Craft Certificate Examination (FCCE), 69 of them passed Physics, 70 passed Technical Drawing and 80 passed Mathematics. Of these, 44 passed both physics and mathematics and 45 passed Technical Drawing and Mathematics. Given that 14 of them passed all the three subjects and 5 failed the three subjects, find the number of students who passed ​

Answer 1

Out of 115 students who sat for the FCCE, 110 students passed at least one subject.

To find the number of students who passed, let's use the principle of inclusion and exclusion.

Let
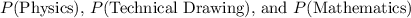`\( P(\text{Physics}) \), \( P(\text{Technical Drawing}) \), and \( P(\text{Mathematics}) \)` represent the number of students who passed Physics, Technical Drawing, and Mathematics, respectively.

Given:

`- \( P(\text{Physics}) = 69 \)`

`- \( P(\text{Technical Drawing}) = 70 \)`

`- \( P(\text{Mathematics}) = 80 \)`

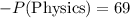
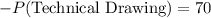
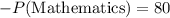
The number of students who passed both Physics and Mathematics
`(\( P(\text{Physics and Mathematics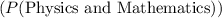}) \))` is 44, and the number of students who passed Technical Drawing and Mathematics
`(\( P(\text{Technical Drawing and Mathematics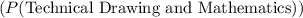}) \))` is 45.

The number of students who passed all three subjects
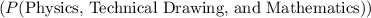`(\( P(\text{Physics, Technical Drawing, and Mathematics}) \))` is 14.

Using the principle of inclusion and exclusion:

• P(Passed at least one subject) = P(Physics) + P(Technical Drawing) + P(Mathematics) - P(Physics and Mathematics) - P(Technical Drawing and Mathematics) + P(Physics, Technical Drawing, and Mathematics)
• 
  `\[ P(\text{Passed at least one subject}) = 69 + 70 + 80 - 44 - 45 + 14 \]`

• 
  `\[ P(\text{Passed at least one subject}) = 144 \]`

Now, subtract the number of students who failed all three subjects
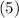`(\( 5 \))` from the total number of students who sat for the examination
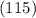`(\( 115 \))` to find the number of students who passed:

`\[ P(\text{Passed}) = 115 - 5 \]`

`\[ P(\text{Passed}) = 110 \]`

Answer 2

Explanation:

what is responsible citizenship