Question

Johnny, of mass 65 kg, and Lucy, of mass 45 kg, are facing each other on roller blades. The coefficient of kinetic friction between the roller blades and concrete surface is 0.20. When Johnny pushes Lucy from rest he applies a force for 1.0 s. Lucy then slows down to a stop in another 8.0 s. Calculate:

a. The applied force exerted by Johnny on Lucy.
b. How long it takes Johnny to come to rest.

I tried calculated the force exerted but I would need acceleration which I don't have...any tips on how to solve this one??? help is appreciated!!

Answer 1

John applied a force of approximately
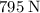`795\; {\rm N}` (on average, rounded) on Lucy.

John slows down to a stop after approximately another
`5.37\; {\rm s}`.

(Assuming that
`g = 9.81\; {\rm N\cdot kg^(-1)}`.)

Step-by-step explanation:

Assuming that the surface is level. The normal force on Johnny will be equal to the weight of Johnny:
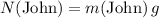`N(\text{John}) = m(\text{John})\, g`. Similarly, the normal force on Lucy will be equal to weight
`N(\text{Lucy}) = m(\text{Lucy})\, g`.

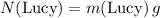Multiply normal force by the coefficient of kinetic friction to find the friction on each person:

`f(\text{John}) = \mu_(k)\, N(\text{John}) = \mu_(k)\, m(\text{John})\, g`.

`f(\text{Lucy}) = \mu_(k)\, N(\text{Lucy}) = \mu_(k)\, m(\text{Lucy})\, g`.

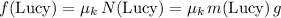Again, because the surface is level, the net force on each person after the first
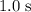`1.0\; {\rm s}` will be equal to the friction. Divide that the net force on each person by the mass of that person to find acceleration:

`\displaystyle a(\text{John}) = \frac{\mu_(k)\, m(\text{John})\, g}{m(\text{John})} = \mu_(k)\, g`.

`\displaystyle a(\text{Lucy}) = \frac{\mu_(k)\, m(\text{Lucy})\, g}{m(\text{Lucy})} = \mu_(k)\, g`.

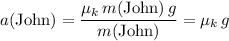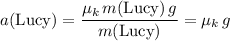(Note that the magnitude of acceleration is independent of mass and is the same for both John and Lucy.)

`a = \mu_(k)\, g= (0.2)\, (9.81\; {\rm m\cdot s^(-2)}) = 1.962\; {\rm m\cdot s^(-2)}`.

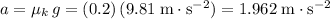In other words, after the first
`1\; {\rm s}`, both John and Lucy will slow down at a rate of
`1.962\; {\rm m\cdot s^(-2)}`.

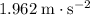To find the speed of Lucy immediately after the first
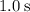`1.0\: {\rm s}`, multiply this acceleration by the time
`t = 8.0\; {\rm s}` it took for Lucy to slow down to
`0\; {\rm m\cdot s^(-1)}`:

`\begin{aligned}& (8.0\; {\rm s})\, (1.962\; {\rm m\cdot s^(-2)}) \\ =\; & (8.0)\, (1.962)\; {\rm m\cdot s^(-1)} \\ =\; & 15.696\; {\rm m\cdot s^(-1)}\end{aligned}`.

Thus, in the first
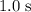`1.0\; {\rm s}`, Lucy accelerated (from
`0\; {\rm m\cdot s^(-1)}`) to
`15.696\; {\rm m\cdot s^(-1)}`.

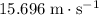The average acceleration of Lucy in the first
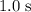`1.0\; {\rm s}` would be
`(15.696) / (1) = 15.696\; {\rm m\cdot s^(-2)}`. Multiply this average acceleration by the mass of Lucy to find the average net force on Lucy during that
`1.0\; {\rm s}`:

`\begin{aligned}F_{\text{net}}(\text{Lucy}) &= m(\text{Lucy})\, a \\ &= (45)\, (15.696)\; {\rm N} \\ &= 706.320\; {\rm N}\end{aligned}`.

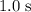This net force on Lucy during that
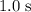`1.0\; {\rm s}` is the combined result of both the push from Johnny and friction:

`F_{\text{net}}(\text{Lucy}) = F(\text{push}) - f(\text{Lucy})`.

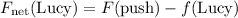Since
`f(\text{Lucy}) = \mu_(k)\, N(\text{Lucy}) = \mu_(k)\, m(\text{Lucy})\, g`:

`\begin{aligned}F(\text{push}) &= F_{\text{net}}(\text{Lucy}) + f(\text{Lucy}) \\ &= F_{\text{net}}(\text{Lucy}) + \mu_(k)\, m(\text{Lucy})\, g \\ &= (706.320) \; {\rm N}+ (0.2)\, (45)\, (9.81)\; {\rm N} \\ &= 706.320\; {\rm N} + 88.290\; {\rm N} \\ &=794.610\; {\rm N}\end{aligned}`.

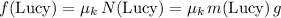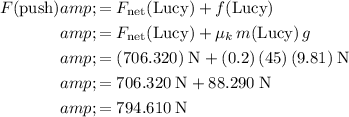In other words, Johnny would have applied a force of
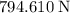`794.610\; {\rm N}` on Lucy.

By Newton's Laws of Motion, when Johnny exerts this force on Lucy in that
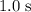`1.0\; {\rm s}`, Lucy would exert a reaction force on Johnny of the same magnitude:
`794.610\; {\rm N}`.

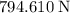Similar to Lucy, the net force on Johnny during that
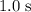`1.0\; {\rm s}` will be the combined effect of the push
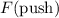`F(\text{push})` and friction
`f(\text{John}) = \mu_(k)\, m(\text{John})\, g`:

`\begin{aligned}F_{\text{net}}(\text{John}) &= F(\text{push}) - f(\text{John}) \\ &= F(\text{push}) - \mu_(k)\, m(\text{John})\, g\\ &= 794.610\; {\rm N} - (0.2)\, (65)\, (9.81)\; {\rm N} \\ &= 667.080\; {\rm N}\end{aligned}`.

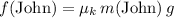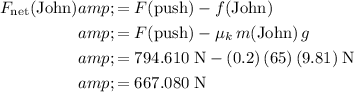Divide net force by mass to find acceleration:

`\begin{aligned}\frac{667.080\; {\rm N}}{65\; {\rm kg}} \approx 10.2628\; {\rm m\cdot s^(-2)}\end{aligned}`.

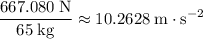In other words, Johnny accelerated at a rate of approximately
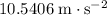`10.5406\; {\rm m\cdot s^(-2)}` during that
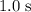`1.0\; {\rm s}`. Assuming that Johnny was initially not moving, the velocity of Johnny right after that
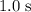`1.0\; {\rm s}\!` would be:

`(0\; {\rm m\cdot s^(-1)}) + (10.2628\; {\rm m\cdot s^(-2)})\, (1.0\; {\rm s}) = 10.2628\; {\rm m\cdot s^(-1)}`.

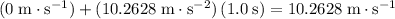After the first
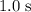`1.0\; {\rm s}`, the acceleration of both John and Lucy (as a result of friction) would both be equal to
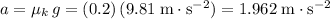`a = \mu_(k)\, g= (0.2)\, (9.81\; {\rm m\cdot s^(-2)}) = 1.962\; {\rm m\cdot s^(-2)}`. Divide initial velocity of Johnny by this acceleration to find the time it took for Johnny to slow down to a stop:

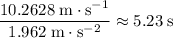`\displaystyle \frac{10.2628\; {\rm {m\cdot s^(-1)}}}{1.962\; {\rm m\cdot s^(-2)}} \approx 5.23\; {\rm s}`.