Answer:
a) 0.34 = 35% probability that at least one member of a married couple will vote.
b) 0.7143 = 71.43% probability that a wife will vote
c) 0.0968 = 9.68% probability that a husband will vote
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is
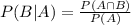
In which
P(B|A) is the probability of event B happening, given that A happened.
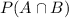 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
This is used for itens B and C. For item a, we treat the probabilities as Venn sets.
A) What is the probability that at least one member of a married couple will vote?
I am going to say that:
Event A: Husband votes.
Event B: Wife votes.
The probability that the husband will vote on a bond referendum is 0.21
This means that
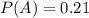
The probability that the wife will vote on the referendum is 0.28
This means that
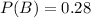
The probability that both the husband and the wife will vote is 0.15.
This means that
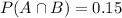
At least one votes:
This is
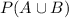 , which is given by:
, which is given by:
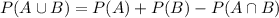
So
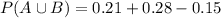
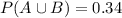
0.34 = 35% probability that at least one member of a married couple will vote.
B) What is the probability that a wife will vote, given that her husband will vote?
Here, we use conditional probability:
Event A: Husband votes:
Event B: Wife votes
The probability that the husband will vote on a bond referendum is 0.21
This means that
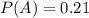
Intersection of events A and B:
Intersection between husband voting and wife voting is both voting, which means that
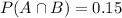
The desired probability is:
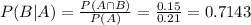
0.7143 = 71.43% probability that a wife will vote.
C) What is the probability that a husband will vote, given that his wife does not vote?
Event A: Wife does not vote.
Event B: Husband votes.
The probability that the wife will vote on the referendum is 0.28
So 1 - 0.28 = 0.62 probability that she does not vote, which means that
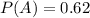
Probability of husband voting and wife not voting:
0.21 probability husband votes, 0.15 probability wife votes, so 0.21 - 0.15 = 0.06 probability husband votes and wife does not, so
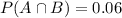
The desired probability is:
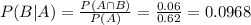
0.0968 = 9.68% probability that a husband will vote