Question

Please help quick!!

A person invests 2000 dollars in a bank. The bank pays 6.75% interest compounded
monthly. To the nearest tenth of a year, how long must the person leave the money
in the bank until it reaches 2900 dollars?

Answer 1

Given that,

Principal amount, P = 2000 dollars

Rate of interest, r = 6.75% = 0.0675

Final amount, A = 2900 dollars

The formula to find the final amount in a compound interest is,

A = P (1 +
`(r)/(n)` )^ (nt)

n = number of times interest compounded in a year = 12 (Since compounded monthly.

Substituting the given values,

`2900 = 2000 \huge \text[1 + \huge \text((0.0675)/(12) \huge \text)\huge \text]^((12t))`

`2900 = 2000 (1.005625)^{(12t)`

`2900 = 2000 (1.069628)^t`

`(1.069628)^t = 1.45`

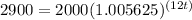
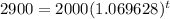
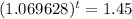
Taking logarithms on both sides,

`\text{t} =\frac{\text{log}(1.45)}{\text{log}(1.069628)}`

`\boxed{\bold{t = 5.52 \thickapprox 5.5}}`

Hence the time that the person must keep the money is 5.5 years.