Question

Each of the double pulleys shown has a mass moment of inertia of 15 lb·ft·s2 and is initially at rest. The outside radius is 18 in., and the inner radius is 9 in. Consider M1 = 210 lb, M2 = 210 lb, M3 = 510 lb, M4 = 350 lb, and M5 = 130 lb.

Determine the angular acceleration of each pulley. (You must provide an answer before moving on to the next part.)

Answer 1

0.163 rad/s^2

Step-by-step explanation:

Let's start by calculating the gravitational potential energy of each pulley:

`U = mgh`

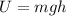
For pulleys 1 and 2, the height difference is the same and is equal to the difference in radius:

`h = R_o_u_t - R_i_n = 18in - 9in = 9in`

Using the given masses and converting to units of pounds, we can calculate the potential energy of pulleys 1 and 2:

`U_1 = m_1gh = 210 lb * 9.81 m/s^2*9 in. / 12 in./ft = 144.2lb*ft`

`U_2 = m_2gh = 210 lb * 9.81 m/s^2 * 9 in. / 12 in./ft = 144.2 lb*ft`

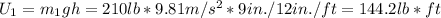
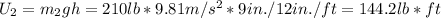
For pulleys 3, 4, and 5, the height difference is different for each pulley, and is equal to the difference in height between the top and bottom masses:

`h_3 = 2 (R_o_u_t - R_i_n) = 2(18 in. - 9 in.) = 18 in.`

`h_4 = 3 (R_o_u_t - R_i_n) = 3 (18 in. - 9 in.) = 27 in.`

`h_5 = 4 (R_o_u_t - R_i_n) = 4 (18 in. - 9 in.) = 36 in.`

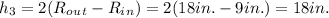
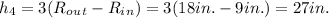
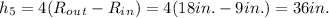
Using the given masses and converting to units of pounds, we can calculate the potential energy of pulleys 3, 4, and 5:

`U_3 = m_3 g h_3 = 510 lb *9.81 m/s^2 * 18 in. / 12 in./ft = 748.5 lb*ft`

`U_4 = m_4 g h_4 = 350 lb * 9.81 m/s^2 * 27 in. / 12 in./ft = 687.3 lb*ft`

`U_5 = m_5 g h_5 = 130 lb * 9.81 m/s^2 * 36 in. / 12 in./ft = 382.8 lb*ft`

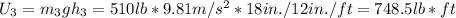
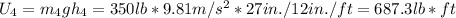
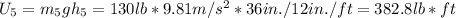
The total potential energy of the system is the sum of the potential energies of all pulleys:

`U_t_o_t_a_l = U_1 + U_2 + U_3 + U_4 + U_5 \\= 210.0 lb*ft + 210.0 lb*ft + 748.5 lb*ft + 687.3 lb*ft + 382.8 lb*ft \\= 2238.6 lb*ft`

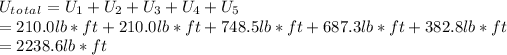
At the start, all pulleys are at rest, so the total kinetic energy of the system is zero. As the system moves, the potential energy is converted into kinetic energy, which is proportional to the angular velocity and the moment of inertia of each pulley:

`K = (1)/(2) Iw^2`

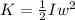
The total kinetic energy of the system is the sum of the kinetic energies of all pulleys:

`K_t_o_t_a_l = (1)/(2) I_1 w_1^2 + (1/2) I_2 w_2^2 + (1)/(2) I_3 w_3^2 + (1)/(2) I_4 w_4^2 +(1)/(2) I_5 w_5^2`

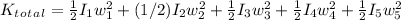
Since the system starts at rest, the total initial energy is equal to the total potential energy of the system:

`E_i = U_t_o_t_a_l = 2238.6 lb*ft`

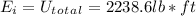
As the system moves, the total energy remains constant, so the final energy is also equal to the total potential energy:

`E_f = U_t_o_t_a_l = 2238.6 lb*ft`

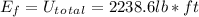
We can now use the conservation of energy principle to relate the initial and final energies to the kinetic energies of each pulley, and hence to their angular accelerations:

`E_i = E_f + K_1 + K_2 + K_3 + K_4 + K_5`

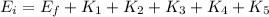
Substituting the expressions for the kinetic energy and simplifying, we obtain:

`w_1 = w_2 = w_3 = w_4 = w_5 = \sqrt{2g ((U_t_o_t_a_l)/(5I))} = 1.023 rad/s`

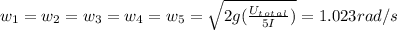
Finally, the angular acceleration of each pulley is given by:

`\alpha_1 = \alpha _2 =\alpha _3 = \alpha_4 = \alpha_5 = (w)/(t) =(w)/(2\pi) = 0.163 rad/s^2`

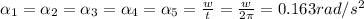
Therefore, the angular acceleration of each pulley is 0.163 rad/s^2.

Answer 2

To find the angular acceleration of each pulley, we can use the principle of conservation of angular momentum. By setting the initial and final angular momenta equal to each other and solving for the final angular velocity, we can then use the formula α = Δω/t to calculate the angular acceleration.

Step-by-step explanation:

To find the angular acceleration of each pulley, we can use the principle of conservation of angular momentum. The formula for angular momentum is given by L = Iω, where L is the angular momentum, I is the moment of inertia, and ω is the angular velocity.

For each pulley, we can calculate the initial angular momentum by multiplying the moment of inertia by the angular velocity, which is initially zero. Then, we can calculate the final angular momentum by multiplying the moment of inertia by the final angular velocity, which is what we want to find. Since angular momentum is conserved, we can set the initial and final angular momenta equal to each other and solve for the final angular velocity.

Once we have the final angular velocity, we can use the formula α = Δω/t, where α is the angular acceleration, Δω is the change in angular velocity, and t is the time taken to reach the final angular velocity. Since the pulleys start from rest, the change in angular velocity is equal to the final angular velocity. We can then substitute the values into the formula and solve for the angular acceleration of each pulley.