Question

Find the partial fraction decomposition of 15/(x-7)(x+3)

Answer 1

`(15)/((x-7)*(x+3)) = (3/2)/(x-7) + (-3/2)/(x+3)`

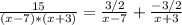
Explanation:

Set up the partial fraction decomp:

`(15)/((x-7)*(x+3)) = (A)/(x-7) + (B)/(x+3)\\`

Multiply across:

`15 = ((A)/(x-7) + (B)/(x+3))*(x+3)*(x-7)\\15 = A(x+3) + B(x-7)\\`

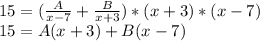
You can do this two ways from this point, you can plug in values for x to solve for A and B individually or set up a system of equations to find A and B

`15 = Ax + 3A + Bx -7B\\Ax + Bx = 0\\3A - 7B = 15\\`

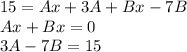
From the first equation we can see that A = -B, plugging into the second equation we get that

-10B = 15, so therefore B = -3/2 and because of the first equation A = 3/2 giving us our answer