Answer:
Approximately
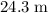 .
.
Step-by-step explanation:
Under the assumptions, the net force on the block is equal to the horizontal force from the worker.
During the first
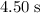 where the worker was applying a constant force on the block, the net force on the block will be constant. Acceleration of the block will be also constant, and SUVAT equations will apply.
where the worker was applying a constant force on the block, the net force on the block will be constant. Acceleration of the block will be also constant, and SUVAT equations will apply.
Apply the SUVAT equation:
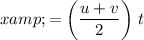 ,
,
Where:
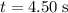 is the duration of the acceleration,
is the duration of the acceleration,
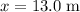 is the displacement of the block during that
is the displacement of the block during that
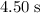 ,
,
 is the initial velocity of the block (the block started from rest,) and
is the initial velocity of the block (the block started from rest,) and
 is the velocity of the block after the
is the velocity of the block after the
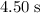 of acceleration.
of acceleration.
(In other words, displacement during constant acceleration is equal to average velocity times the duration of the acceleration.)
Rearrange this equation to find
 :
:
 .
.
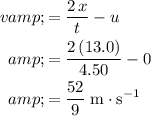 .
.
During the next
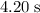 , the net force on the block will be zero. The velocity of the block during that much time will stay unchanged at the final velocity after the initial
, the net force on the block will be zero. The velocity of the block during that much time will stay unchanged at the final velocity after the initial
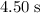 , which is
, which is
 .
.
Since velocity during this
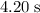 is constant, simply multiply that velocity by the duration to find the distance travelled:
is constant, simply multiply that velocity by the duration to find the distance travelled:
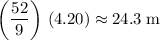 .
.
In other words, the block would have travelled an additional
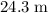 during the
during the
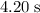 .
.