23. By the diagram, the triangle is a
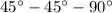 triangle. Therefore, the triangle is isosceles, so
triangle. Therefore, the triangle is isosceles, so
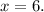 And by the Pythagorean theorem,
And by the Pythagorean theorem,
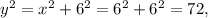 and taking the square root yields
and taking the square root yields
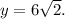
24. Notice that by the diagram, the triangle is a
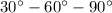 triangle. It is well known that in these special types of triangles, if
triangle. It is well known that in these special types of triangles, if
 is the side length opposite the
is the side length opposite the
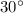 angle, then the side length opposite the
angle, then the side length opposite the
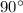 angle is
angle is
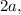 and finally the side length opposite the
and finally the side length opposite the
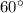 is
is
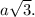 This is shown in the image I've attached below, and can also be easily proven by the fact that two of these triangles combine to form an equilateral triangle.
This is shown in the image I've attached below, and can also be easily proven by the fact that two of these triangles combine to form an equilateral triangle.
So using this fact, we know that
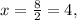 and
and
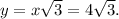
25. Tell whether the given side lengths can represent the sides of a right triangle: 10, 12, 20
For this question, we simply use the converse of the Pythagorean theorem. One part of its statement says that if a triangle has sides of length
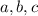 such that
such that
 , and
, and
 is the longest side, then the angle opposite the side of length
is the longest side, then the angle opposite the side of length
 is a right angle.
is a right angle.
Thus, if the triple
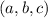 does not satisfy the equation, the triangle it forms is not a right triangle. In our case, the corresponding values for
does not satisfy the equation, the triangle it forms is not a right triangle. In our case, the corresponding values for
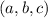 are
are
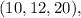 because
because
 is the largest number in this triple. But
is the largest number in this triple. But
 so the triangle with side lengths
so the triangle with side lengths
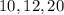 is not a right triangle.
is not a right triangle.
26. Another statement of the converse of the Pythagorean theorem is that if a triangle has side lengths
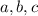 such that
such that
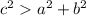 , with
, with
 being the longest side, then the triangle is an obtuse triangle. So the corresponding values for
being the longest side, then the triangle is an obtuse triangle. So the corresponding values for
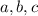 are
are
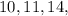 and because
and because
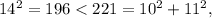 the triangle is an obtuse triangle.
the triangle is an obtuse triangle.