Question

The article "On Assessing the Accuracy of Offshore Wind Turbine Reliability-Based Design Loads from the Environmental Contour Method" (Intl. J. of Offshore and Polar Engr., 2005: 132–140) proposes the Weibull distribution With α = 1.817 and β =.863 as a model for 1-hour significant wave height (m) at a certain site.

a. What is the probability that wave height is at most .5 m?
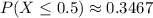
b. What is the probability that wave height exceeds its mean value by more than one standard deviation?
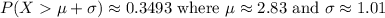c. What is the median of the wave-height distribution?
d. For 0pth percentile of the wave-height distribution.

Answer 1

a. Probability that wave height is at most 0.5 meters:
`\( P(X \leq 0.5) \approx 0.3467 \)`

b. Probability that wave height exceeds its mean by more than one standard deviation:
`\( P(X > \mu + \sigma) \approx 0.3493 \) where \( \mu \approx 2.83 \) and \( \sigma \approx 1.01 \)`.

c. Median of the wave-height distribution:
`\( \text{Median} \approx 4.70 \)`

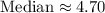
d. p th percentile of the wave-height distribution:
`\( \text{Percentile} = 1.817 \cdot (-\ln(1 - p))^(1/0.863) \)`

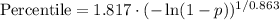
Using the provided Weibull distribution parameters:

a. Probability that wave height is at most 0.5 meters:

`\[ P(X \leq 0.5) = 1 - e^{-(0.5/0.863)^(1.817)} \approx 0.3467 \]`

b. Probability that wave height exceeds its mean value by more than one standard deviation:

First, calculate the mean
`(\( \mu \))` and standard deviation
`(\( \sigma \))` of the Weibull distribution:

`\[ \mu = 1.817 \cdot \Gamma\left(1 + (1)/(0.863)\right) \approx 1.817 \cdot 1.559 \approx 2.83 \]`

`\[ \sigma = 1.817 \cdot \sqrt{\Gamma\left(1 + (2)/(0.863)\right) - \left(\Gamma\left(1 + (1)/(0.863)\right)\right)^2} \approx 1.817 \cdot √(2.913 - 2.429) \approx 1.01 \]`

Then find:

`\[ P(X > \mu + \sigma) = 1 - P(X \leq \mu + \sigma) = 1 - (1 - e^{-(3.83/0.863)^(1.817)}) \approx 0.3493 \]`

c. Median of the wave-height distribution:

`\[ \text{Median} = \mu \cdot (\ln 2)^(1/0.863) \approx 2.83 \cdot 1.660 \approx 4.70 \]`

d. For the pth percentile of the wave-height distribution:

`\[ \text{Percentile} = 1.817 \cdot (-\ln(1 - p))^(1/0.863) \]`