The limit as x approaches ∞ for f(x) is ∞, while as x approaches -∞, f(x) approaches 0. f(x) is increasing for all x and is never concave downward for any interval.
(a) To find
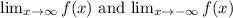 :
:
![\[f(x) = (x^2 - 2x - 1)e^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h4qumbjn6c8p4s7rjw51rjmfvo381qr1qf.png)
As x approaches positive or negative infinity, the behavior of the exponential term
 dominates. Since
dominates. Since
 grows without bound as x goes to infinity and approaches zero as x goes to negative infinity, the limits will be determined by the behavior of
grows without bound as x goes to infinity and approaches zero as x goes to negative infinity, the limits will be determined by the behavior of
 .
.
Therefore:
-
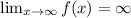 because
because
 grows without bound as x approaches infinity.
grows without bound as x approaches infinity.
-
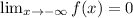 because
because
 approaches zero as x approaches negative infinity.
approaches zero as x approaches negative infinity.
(b) To find the intervals on which f is increasing, we'll find the derivative of f(x) and then determine where the derivative is positive:
Given:
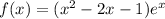
Let's find f'(x) (the derivative of f(x)) using the product rule and determine its sign:
![\[f'(x) = (2x - 2)e^x + (x^2 - 2x - 1)e^x = (x^2 + 1)e^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/39gzc8w4901y4lu99qd1p0v6emilijtw6m.png)
For f'(x) to be positive,
 must be positive (as
must be positive (as
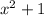 is always positive). Since
is always positive). Since
 is positive for all real values of x, f'(x) will be positive for all real values of x.
is positive for all real values of x, f'(x) will be positive for all real values of x.
Therefore, f(x) is increasing for all real values of x.
(c) To find the intervals on which the graph of f is concave downward, we'll find the second derivative of f(x) and determine where it's negative:
Given:
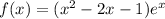
Let's find f''(x) (the second derivative of f(x):
![\[f'(x) = (x^2 + 1)e^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kjrdi26z2ihzixf3h615rgmxpx5ehf4uso.png)
![\[f''(x) = (2x)e^x + (x^2 + 1)e^x = (x^2 + 2x + 1)e^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r72z5tyjmuqbff525wuk4ga4pdvisst4jx.png)
For f''(x) to be negative,
 must be negative. Factoring
must be negative. Factoring
 gives us
gives us
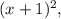 which is always non-negative.
which is always non-negative.
Therefore, f''(x) is never negative for any real value of x, which means that the graph of f is never concave downward for any interval. It is either concave upward or has points of inflection but never concave downward for any interval.
(d)
Question:
Let f be the function given by f(x) = (x² - 2x - 1)eˣ.
(a) Find
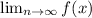 and
and
 .
.
(b) Find the intervals on which f is increasing. Show the analysis that leads to your answer.
(c) Find the intervals on which the graph off is concave downward. Show the analysis that leads to your answer.
(d) Sketch the graph of f.