Question

Ahmed is modelling the area covered by a moss using the equation A = t² + 5.8t +

9.41 where A is the area covered in square centimeters, negative values of t represent
a number of days after noon on July 1, 2014. Which of the following equivalent
expressions contain the number of days before noon on July 1, 2014, as a constant or
coefficient, when the moss started with its smallest area of 1 square centimeter?
a.(t − (−2.9))² + 1
b. (t−(−1))² +3.8t +8.41
c.(t-(-3.9)) (t- (-1.9)) + 2
d. t(t− (−5.8)) + 9.41

Answer 1

a. (t - (-2.9))² + 1

Explanation:

We are told that Ahmed is modelling the area covered by a moss using the equation A = t² + 5.8t + 9.41.

The given equation is a quadratic equation with a positive leading coefficient. Therefore, the graph is a parabola that opens upwards. This means that the vertex is its lowest point.

The vertex form of a quadratic equation is:

`\boxed{y = (x - h)^2 + k}`

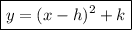
where (h, k) is the vertex.

As the vertex is the lowest point, this means that the y-value of the vertex is when the area of moss is at its lowest. We are told that the smallest area of the moss is 1 square centimeter, so k = 1.

The x-value of the vertex can be found by using the formula:

`h=-(b)/(2a)`

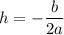
for a quadratic in the form ax² + bx + c.

For the given quadratic, a = 1, b = 5.8 and c = 9.41.

Substitute the values of a and b into the formula to find the x-value of the vertex:

`\implies h=-(5.8)/(2(1))=-2.9`

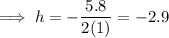
Finally, substitute h = -2.9 and k = 1 into the vertex form:

`A=(t-(-2.9))^2+1`

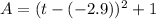
Therefore, the equivalent expression that contains the number of days before noon on July 1, 2014, as a constant or coefficient, when the moss started with its smallest area of 1 square centimeter is:

• (t - (-2.9))² + 1