Question

A cylinder of radius 20m is rolling down with constant speed 80cm/sec what is the rotational speed

Answer 1

The answer to this question is 0.04

Answer 2

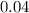`0.04` radians per second.

Step-by-step explanation:

The circumference of this cylinder (radius
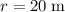`r = 20\; {\rm m}`) is:

`C = 2\, \pi\, r = 40\, \pi\; {\rm m}`.

In other words, this cylinder will travel a linear distance of
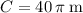`C = 40\, \pi \; {\rm {\rm m}` after every full rotation.

It is given that the cylinder rotates at a rate of
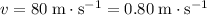`v = 80\; {\rm m\cdot s^(-1)} = 0.80\; {\rm m\cdot s^(-1)}`. Thus:

`\begin{aligned}\frac{0.8\; {\rm m}}{1\; {\rm s}} * \frac{1\; \text{rotation}}{40\, \pi\; {\rm m}}\end{aligned}`.

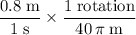Additionally, each full rotation is
`2\, \pi` radians in angular displacement. Combining all these parts to obtain the rotation speed of this cylinder:

`\begin{aligned}\frac{0.8\; {\rm m}}{1\; {\rm s}} * \frac{1\; \text{rotation}}{40\, \pi\; {\rm m}} * \frac{2\, \pi}{1\;\text{rotation}} = 0.04\; {\rm s^(-1)}\end{aligned}` (radians per second.)