Question

State if the triangle is acute obtuse or right

Answer 1

➛ The given triangle is a right angle triangle.

➛ Option D) 6.3 in is the correct answer.

Step-by-step explanation :

Here we can see that the one angle of triangle is 90⁰. Therefore, it's a right angle triangle.

Now, Here we have given that the base and altitude of triangle and we need to find the hypotenuse of triangle.

• ↠ Base = 4.8 in
• ↠ Altitude = 4.1 in
• ↠ Hypotenuse = x

So, by using Pythagoras Theorem we will find the hypotenuse of triangle :

`\sf{\longrightarrow{{(Hypotenuse)}^(2) = {(Altitude)}^(2) + {(Base)}^(2)}}`

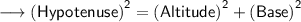
Substituting all the given values in the formula to find hypotenuse :

`\sf{\longrightarrow{{(x)}^(2) = {(4.1)}^(2) + {(4.8)}^(2)}}`

`\sf{\longrightarrow{{(x)}^(2) = {(4.1 * 4.1)} + {(4.8 * 4.8)}}}`

`\sf{\longrightarrow{{(x)}^(2) = {(16.81)} + {(23.04)}}}`

`\sf{\longrightarrow{{(x)}^(2) = 16.81 + 23.04}}`

`\sf{\longrightarrow{{(x)}^(2) = 39.85}}`

`\sf{\longrightarrow{x = √(39.85)}}`

`\sf{\longrightarrow{\underline{\underline{x \approx 6.3 \: in}}}}`

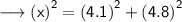
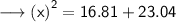
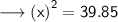
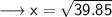
Hence, the value of x is 6.3 in.

————————————————

Answer 2

right

D. 6.3 m

Explanation:

You want to know if the given triangle is acute, obtuse, or right, and the value of x.

Triangle

The red icon in the corner indicates the triangle is a right triangle. The Pythagorean theorem applies, so ...

x² = 4.8² +4.1² = 39.85

x = √39.85 ≈ 6.3

The value of x in this right triangle is about 6.3 m.

__

Additional comment

The triangle cannot be solved for the remaining side unless you know at least one angle. The marked right angle is sufficient to let you solve for x.