Question

What does this problem mean |x+3| if x>5

Answer 1

x+3 . . . . if x > 5

Explanation:

You want the meaning of |x+3| if x > 5.

Absolute value

The absolute value function is a piecewise defined function:

`y=|x|=\begin{cases}-x&\text{for }x < 0\\x&\text{for }x\ge0\end{cases}`

Application

The expression (x+3) is zero when x=-3. So, your absolute value function will have the piecewise definition ...

`|x+3|=\begin{cases}-(x+3)&\text{for }x < -3\\x+3&\text{for }x\ge-3\end{cases}`

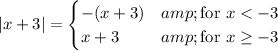
You are interested in the value for x > 5, which is definitely greater than -3. That means only the second part of this definition is applicable.

x+3 . . . . if x > 5

__

Additional comment

The attache graph shows the given absolute value expression (dashed red line). The blue line is (x+3) for x > 5. You can see that it matches the given expression in that region.