This question is incomplete, the complete question is;
Suppose u and v are functions of x that are differentiable at x=0
and that { u(0) = 7, u'(0) = -5 } { v(0)= -1, v'(0) = -4 }
Find the values of the following derivatives at x = 0.
a)
 ( uv )
( uv )
b)
 (
(
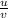 )
)
c)
 (
(
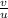 )
)
Answer:
a)
 ( uv ) = -23
( uv ) = -23
b)
 (
(
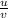 ) = 33
) = 33
c)
 (
(
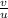 ) = -32/49 or - 0.6531
) = -32/49 or - 0.6531
Explanation:
Given that;
{ u(0) = 7, u'(0) = -5 } { v(0)= -1, v'(0) = -4 }
a)
 ( uv )
( uv )
we differentiate
 ( uv ) = uv' + vu'
( uv ) = uv' + vu'
at x = (0), we substitute our values
 ( uv ) = ( 7 × -4 ) + ( -1 × -5)
( uv ) = ( 7 × -4 ) + ( -1 × -5)
 ( uv ) = -28 + 5
( uv ) = -28 + 5
 ( uv ) = -23
( uv ) = -23
b)
 (
(
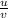 )
)
we differentiate
 (
(
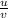 ) = ( vu' - uv' ) / v²
) = ( vu' - uv' ) / v²
at x=0, we substitute our values
 (
(
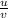 ) = ( (-1 × -5) - (7 × -4 ) ) / (-1)²
) = ( (-1 × -5) - (7 × -4 ) ) / (-1)²
 (
(
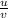 ) = (( 5 - ( -28 )) / 1
) = (( 5 - ( -28 )) / 1
 (
(
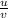 ) = 33 / 1
) = 33 / 1
 (
(
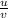 ) = 33
) = 33
c)
 (
(
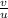 )
)
we differentiate
 (
(
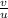 ) = ( uv' - vu' ) / u²
) = ( uv' - vu' ) / u²
at x=0, we substitute our values
 (
(
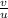 ) = ( (7 × -4) - (-1 × -4) ) / (7)²
) = ( (7 × -4) - (-1 × -4) ) / (7)²
 (
(
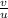 ) = ( -28 - ( 4 ) ) / 49
) = ( -28 - ( 4 ) ) / 49
 (
(
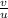 ) = ( -28 - 4 ) /49
) = ( -28 - 4 ) /49
 (
(
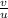 ) = -32 / 49
) = -32 / 49
 (
(
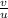 ) = -32/49 or - 0.6531
) = -32/49 or - 0.6531