Answer:
A.
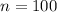
B.
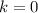
Explanation:
A. The equation "110% n = 11" can be solved as follows:
110% n = 11
To solve for n, we need to get rid of the percentage sign (%). We can do this by dividing both sides of the equation by 110%, or 0.110 (since 110% is equivalent to 1.1 in decimal form).
(110% n) / 110% = 11 / 110%
n = 11 / 0.110
n = 100
So, the solution for n in the equation "110% n = 11" is n = 100.
B. The given equation is:
(328 x 128) x k = 328 x (82 x 128) x k
To solve for k, we can simplify the equation using the properties of multiplication.
Step 1: Perform the multiplications inside the parentheses:
41984 x k = 328 x 10576 x k
Step 2: Rearrange the equation by applying the associative property of multiplication:
41984 x k = 328 x (10576 x k)
Step 3: Divide both sides of the equation by 328:
(41984 x k) / 328 = 10576 x k
Step 4: Cancel out the common factor of k on the left-hand side:
(41984 / 328) x k = 10576 x k
Step 5: Simplify the left-hand side:
128 x k = 10576 x k
Step 6: Subtract 10576 x k from both sides of the equation to isolate k:
128 x k - 10576 x k = 0
Step 7: Factor out k on the left-hand side:
k x (128 - 10576) = 0
Step 8: Simplify further:
k x (-10448) = 0
Step 9: Divide both sides of the equation by (-10448):
k = 0
So, the solution for k in the equation "(328 x 128) x k = 328 x (82 x 128) x k" is k = 0.