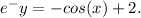Question

Using separation of variables technique, solve the following differential equation with initial condition y, = ey sin, and y(-r)-0. The solution is: ? A. e-y =-sinx +2 B. e-y = -cosx +2 C. e-y = cosx +2 D. ey = cosx +2 E. e-y = cosx

Answer 1

To solve the given differential equation using separation of variables, we start by separating the variables and integrating. The solution is y = ± C0 e^(-cos x).

Step-by-step explanation:

To solve the given differential equation using separation of variables, we start by separating the variables and integrating. We have:

y' = ey sin x

Dividing both sides by ey gives:

(1/y) dy = sin x dx

Integrating both sides gives:

ln|y| = -cos x + C

where C is the constant of integration. Exponentiating both sides gives:

|y| = e^(-cos x + C)

Since C is an arbitrary constant, we can write it as C = ln|C0| where C0 is another constant. Therefore, the solution to the differential equation is:

|y| = e^(-cos x + ln|C0|)

Using the property of logarithms, we can simplify the solution to:

|y| = C0 e^(-cos x)

Since we have an absolute value on the left side, we can split the solution into two cases:

y = C0 e^(-cos x) or y = -C0 e^(-cos x)

And we can write it as:

y = ± C0 e^(-cos x)

Answer 2

Integrating both sides of the equation and apply the initial condition to find the solution. The correct solution is B.

`e^-y = -cos(x) + 2.`

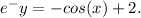
Step-by-step explanation:

To solve the given differential equation using the separation of variables technique, we start by separating the variables y and x. We have
`y' = e^y sin(x).`

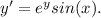
Next, we can divide both sides by e^y sin(x) to isolate the y variable on one side and the x variable on the other side.

This gives us:
`dy/e^y = sin(x)dx.`

Next, we can integrate both sides of the equation. On the left side, we integrate with respect to y, and on the right side, we integrate with respect to x. Thus, we have:
`-e^-y = -cos(x) + C.`

Applying the initial condition y(-r) = 0, we can substitute this into the equation and solve for C. We obtain:
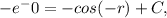`-e^-0 = -cos(-r) + C,` which simplifies to:
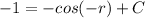`-1 = -cos(-r) + C`. From here, we can solve for C to get C = -1 + cos(-r).

Therefore, the solution to the given differential equation with the initial condition y(-r) = 0 is e^-y = -cos(x) + 2. So, the correct answer is B.

`e^-y = -cos(x) + 2.`