Question

URGENT !

Please see attachment !

Answer 1

68.5 m² (3 s.f.)

Explanation:

OA and OC are radii of the circle with center O.

As BA and BC are tangents to the circle, and the tangent of a circle is always perpendicular to the radius, the measures of ∠OAB and ∠OCB are both 90°.

The sum of the interior angles of a quadrilateral is 360°. Therefore:

`\begin{aligned}m \angle OAB + m \angle OCB + m \angle AOC + m \angle ABC &= 360^(\circ)\\90^(\circ) + 90^(\circ) + 120^(\circ) + m \angle ABC &= 360^(\circ)\\300^(\circ) + m \angle ABC &= 360^(\circ)\\m \angle ABC &= 60^(\circ)\end{aligned}`

The line OB bisects ∠AOC and ∠ABC to create two congruent right triangles with interior angles 30°, 60° and 90°. (See attached diagram).

Therefore triangles BOA and BOC are 30-60-90 triangles.

This means their sides are in the ratio 1 : √3 : 2 = OA : AB : OB.

Therefore, as OA = 10 m, then AB = 10√3 m and OB = 20 m.

The area of triangle BOA is:

`\begin{aligned}\textsf{Area\;$\triangle\;BOA$}&=(1)/(2) \cdot OA \cdot AB\\\\&= (1)/(2) \cdot 10 \cdot 10√(3)\\\\&= 50√(3)\;\sf m^2\end{aligned}`

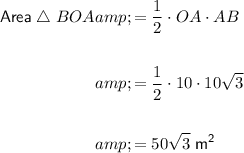
As triangle BOA is congruent to triangle BOC, the area of kite ABCO is:

`\begin{aligned}\textsf{Area\;of\;kite\;$ABCO$}&=2 \cdot 50√(3)\\&=100√(3)\;\sf m^2\end{aligned}`

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left((\theta)/(360^(\circ))\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

Given the angle of the sector is 120° and the radius is 10 m, the area of sector AOC is:

`\begin{aligned}\textsf{Area\;of\;sector\;$AOC$}&=\left((120^(\circ))/(360^(\circ))\right) \pi \cdot 10^2\\\\&=(1)/(3)\pi \cdot 100\\\\&=(100)/(3)\pi\; \sf m^2 \end{aligned}`

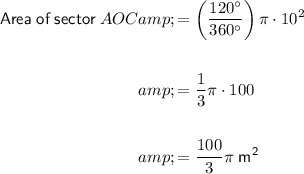
The area of the shaded region is the area of kite ABCO less the area of sector AOC:

`\begin{aligned}\textsf{Area\;of\;shaded\;region}&=100√(3)-(100)/(3)\pi\\&=68.4853256...\\&=68.5\;\sf m^2\;(3\;s.f.)\end{aligned}`

Therefore, the area of the shaded region is 68.5 m² (3 s.f.).