Answer:
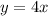
Explanation:
In this question, we are asked to find the rectangular equation of the curve defined by the polar expression:

To achieve this, we can use the polar conversion formulas:
 ... also written as
... also written as
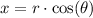
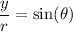 ... also written as
... also written as
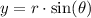
First, we need to form an equation by setting the expression equal to 0.
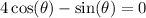
Next, we can substitute for sine and cosine using the above conversion formulas:

From here, we can multiply both sides by r to get rid of the fractions.
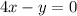
Finally, we can add y to both sides to put the equation in slope-intercept form.
