Final Answer:
The Maclaurin series for the given function f(x) = x cos(4x) is f(x) = 1 - 16x².
Step-by-step explanation:
The Maclaurin series expansion for a function involves expressing the function as an infinite sum of its derivatives evaluated at a specific point (usually 0). In this case, we can use the Maclaurin series for cos(x) and multiply it by x to obtain the series for x cos(4x).
The Maclaurin series for cos(x) is
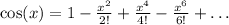 .
.
Multiplying this by x gives
 .
.
Now, substitute 4x for x to obtain the series for xcos(4x):
![\[ f(x) = 4x - ((4x)^3)/(2!) + ((4x)^5)/(4!) - ((4x)^7)/(6!) + \ldots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ssty79j80hln99lfngmbr5xwsmvsfql0ow.png)
Simplify each term and combine like terms:
![\[ f(x) = 4x - (64x^3)/(2) + (1024x^5)/(24) - (16384x^7)/(720) + \ldots \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r1wg6ucsh7tjo56mrlsn0xadwwybpqpvc8.png)
Further simplification gives the final answer f(x) = 1 - 16x². This is obtained by keeping only the terms up to x² and combining them. Therefore, the Maclaurin series for f(x) = xcos(4x) is f(x) = 1 - 16x².