Question

A certain department store keeps track of an age and an annual income of customers who have its credit card. From a sample of 820 of such customers the following descriptive statistics had been obtained: the average age was 41 years with the standard deviation of 16 years and the average annual income was $37,290 with the standard deviation of $2,850. The correlation between the age the annual income was found to be 0.34. Answer the following questions. (Round your answers to 2 places after the decimal point).

Calculate the value of a slope.
a) 309.23 $ per year of age
b) 60.56 $ per year of age
c) 192.43$ per year of age
d) None of the above

Answer 1

Answer: b) $60.56 per year of age

Explanation: If the scatterplot of two variables shows a line and the correlation between them is strong, we can calculate a regression line.

Regression line is a line graph that best fits the data. Like any other line, its formula is given by

y = mx + b

with

m being the slope

b the y-intercept

The slope of the line, correlation and standard deviations of the two variables have the following relationship:

`m=r(S_(y))/(S_(x))`

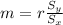
where

r is correlation

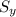`S_(y)` is standard deviation for the y data

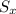`S_(x)` is standard deviation for the x data

For our problem:

r = 0.34

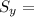`S_(y)=` 2850

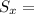`S_(x)=` 16

Calculating

`m=0.34((2850)/(16))`

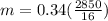
m = 60.56

Slope for the regression line of annual income per year of age is 60.56.