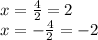Question

Solve the system: xy=4 x^2+y^2=8

Answer 1

Explanation:

`xy=4\\x^(2) +y^(2) =8`

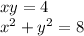
We isolate x and then replace it in the other equation

`x=(4)/(y)`

`((4)/(y))^(2) +y^(2)=8` -->
`(16)/(y^(2)) + y^(2) =8`

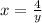
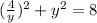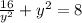
In the end, you have

`(16)/(y^(2) ) +(y^(4) )/(y^(2))=(8y^(2) )/(y^(2) ) \\`

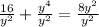
You now multiply y² in both sides so that in the end there is

`16+y^(4)=8y^(2)`

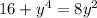
Next step:

`y^(4)-8y^(2)+16=0`

`y^(2) =a`

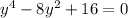
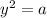
You substitute a in the equation

`a^(2) -8a+16=0`

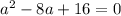
Now, as you can see

`a^(2) -8a+16=(a-4)^(2)`

The result is that
`a=4`

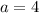
Therefore,

`y=2\\y=-2`

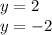
In the
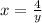`x=(4)/(y)` equation you substitute both values of y

`x=(4)/(2) =2\\x=-(4)/(2) =-2`