Question

A 5.25 L container of ammonia gas exerts a pressure of 652 mm Hg at a temperature of 243 K. Calculate the pressure of this same amount of gas in a

3.50 L container at a temperature of 221 K.

Show your work

Answer 1

889.46 mmHg (2 d.p.)

Step-by-step explanation:

Since we are dealing with the same amount of gas, but at different temperatures and volumes, we can use the combined gas law.

Combined Gas Law

`\boxed{\sf (P_1V_1)/(T_1)=(P_2V_2)/(T_2)}`

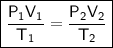
where:

• P₁ is the initial pressure.
• V₁ is the initial volume.
• T₁ is the initial temperature (in kelvin).
• P₂ is the final pressure.
• V₂ is the final volume.
• T₂ is the final temperature (in kelvin).

As we want to find the final pressure, rearrange the formula to isolate P₂:

`\sf P_2=(P_1V_1T_2)/(T_1V_2)`

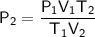
The given values are:

• P₁ = 652 mmHg
• V₁ = 5.25 L
• T₁ = 243 K
• V₂ = 3.50 L
• T₂ = 221 K

Substitute the values into the formula and solve for P₂:

`\implies \sf P_2=(652 \cdot 5.25 \cdot 221)/(243 \cdot 3.50)`

`\implies \sf P_2=(756483)/(850.5)`

`\implies \sf P_2=889.456790...`

`\implies \sf P_2=889.46\;mmHg\;(2\;d.p.)`

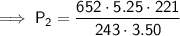
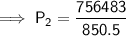
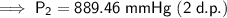
Therefore, the final pressure of the same amount of ammonia gas in a 3.50 L container at a temperature of 221 K is 889.46 mmHg (2 d.p.).