Question

A company manufactures aluminum mailboxes in the shape of a box with a half-cylinder top. The company will make 1927 mailboxes this week. If each mailbox has dimensions as shown in the figure below, how many square meters of aluminum will be needed to make these mailboxes? In your calculations, use the value for 3.14 , and round up your answer to the next square meter.

Answer 1

Explanation:

first we need to find how many square metres of aluminum we need to make 1 mailbox. to find the surface area of the mailbox we seperate it into the bottom cube and the top cylindir. the bottom cubes surface area is

`0.55 * 0.3 + 0.3 * 0.4 * 2 + 0.55 * 0.4 * 2 = 0.165 + 0.24 + 0.44 = {0.845m}^(2)`

the top half cylindirs surface area is

`( {0.3}^(2) * 3.14 / 2 * 2) + (0.3 * 3.14 * 0.55 = {0.2826m}^(2) + {0.5181m}^(2) = {0.8007m}^(2)`

then add both of them together and its

`{0.8007m}^(2) + {0.845m}^(2) = {1.6457m}^(2)`

then multiply that by 1927 and its

`1927 * {1.6457m}^(2) = {3171.2639m}^(2)`

round that up to 3171m squared.

Answer 2

2264 m²

Explanation:

To calculate the total amount of aluminium needed to make the mailboxes, multiply the surface area of one mailbox by the total number of mailboxes.

The surface area of one mailbox is made up of the following areas:

• Rectangular base with dimensions 0.3 m × 0.55 m.
• Two smaller rectangular sides with dimensions 0.3 m × 0.4 m.
• Two larger rectangular sides with dimensions 0.55 m × 0.4 m.
• Two half circular ends. Two half circles make a whole circle. Therefore, the area of the two half circular ends is the area of a circle with diameter 0.3 m. Since the diameter of a circle is twice its radius, the radius of the circle is 0.15 m.
• Half the curved area of a cylinder. The formula for the curved area of a cylinder is 2πrh, so the formula for half the curved area is πrh, where the radius is 0.15 m and the height is 0.55 m.

Calculate the areas:

`\begin{aligned}\textsf{Area of the rectangular base}&=0.3 * 0.55\\&= 0.165\; \sf m^2\end{aligned}`

`\begin{aligned}\textsf{Area of the 2 smaller rectangular sides}&=2(0.3 * 0.4)\\&=2 * 0.12\\&= 0.24 \; \sf m^2 \end{aligned}`

`\begin{aligned}\textsf{Area of the 2 larger rectangular sides}&=2(0.55 * 0.4)\\&=2 * 0.22\\&= 0.44 \; \sf m^2\end{aligned}`

`\begin{aligned}\textsf{Area of the 2 half circular ends}&=\pi r^2\\& = 3.14 * 0.15^2\\&=3.14 * 0.0225\\& = 0.07065 \; \sf m^2\end{aligned}`

`\begin{aligned}\textsf{Area of half the curved area of a cylinder}&=\pi rh\\&= 3.14 * 0.15 * 0.55\\&=0.471 *0.55\\& = 0.25905 \; \sf m^2\end{aligned}`

Sum the areas to find the total surface area of one aluminium mailbox:

`\begin{aligned}\textsf{Total S.A. of one mailbox}&= 0.165 + 0.24 + 0.44 + 0.07065 + 0.25905\\& = 1.1747 \; \sf m^2\end{aligned}`

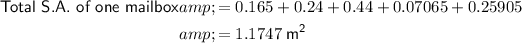
Finally, to calculate the total amount of aluminium needed to make 1927 mailboxes, multiply the surface area of one mailbox by 1927:

`\begin{aligned}\textsf{Aluminium needed to make 1927 mailboxes}&= \textsf{S.A. of one mailbox} * 1927\\&=1.1747 * 1927\\&= 2263.6469\\&= 2264 \; \sf m^2\end{aligned}`

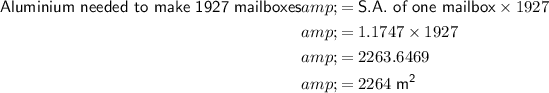
Therefore, 2264 square meters of aluminium will be needed to make 1927 mailboxes (rounded up to the next square meter).