Question

For an angle 0, cos 0 = -1/2 sin 0 > 0.

a. Find 0 in degrees and radians.
b. Find tan 0.

Answer 1

Answer:
`\theta = 120^\circ` and
`\tan(\theta) = -√(3).`

Explanation:

a. We are given that
`\cos(\theta) = -\frac12.` Taking the inverse cosine tells us that the measure of
`\theta` is either 120 or 240 degrees, but because
`\sin(\theta) > 0,` we know that
`0^\circ < \theta < 180^\circ`. Therefore,
`\theta = 120^\circ`.

b. So we know that
`\tan(\theta) = \tan(120^\circ)`, and evaluating this yields
`\tan(\theta) = -√(3).`

Answer 2

`\textsf{a)} \quad \theta=120^(\circ), \quad \theta=(2)/(3)\pi\;\text{(rad)}`

`\textsf{b)} \quad \tan \theta=-√(3)`

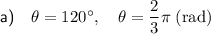
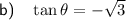
Explanation:

Part (a)

Cosine is negative in quadrants II and III, and sine is positive in quadrants I and II. Therefore, given cos θ = -1/2 and sin θ > 0, then angle θ is in quadrant II.

Using the Pythagorean identity, we can find the value of sin θ:

`\begin{aligned}\sin^2 \theta+\cos^2\theta&=1\\\sin^2 \theta &= 1 - \cos^2 \theta\\\sin^2 \theta &= 1 - \left(-(1)/(2)\right)^2\\\sin^2 \theta &= (3)/(4)\\\sin\theta&=\sqrt{(3)/(4)}\\\sin \theta& = (√(3))/(2)\end{aligned}`

Since angle θ is in quadrant II, we know that it is between 90° and 180°.

In the unit circle, cosine is the x-coordinate of a point on the circle and sine is the y-coordinate of that point.

Therefore, according to the unit circle, the only angle in quadrant II that has a cosine of -1/2 and a sine of √3/2 is 120°.

Therefore, θ = 120°.

To convert degrees to radians multiply the angle in degrees by π/180°.

`\implies \theta=120^(\circ)\cdot (\pi)/(180^(\circ))=(2)/(3)\pi`

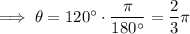
Therefore, angle θ is 120° or 2π/3 radians.

Part (b)

The tangent trigonometric ratio identity is:

`\tan \theta = (\sin \theta)/(\cos \theta)`

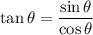
To find the value of tan θ, substitute the values found in part (a) into the identity:

`\begin{aligned}\implies \tan \theta &=((√(3))/(2))/(-(1)/(2))\\\\ &=(√(3))/(-1)\\\\&=-√(3)\end{aligned}`

Therefore, tan θ is -√3.