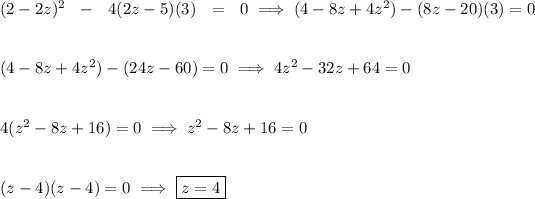Question

For what value(s) of a does the equation (2a-5)x^2 - 2(a-1)x + 3 = 0 have only one rational root?

Answer 1

for the sake of readability, let's change "a" to "z", so for what values of "z" there's only one rational root?

well, we can look at the discriminant of a quadratic, and if the discriminant spits out a 0, or equals 0, then we have only one rational root, so let's reword that.

what values of "z", make the equation 0?

`(2z-5)x^2-2(z-1)x+3=0\implies (2z-5)x^2-(2z-2)x+3=0 \\\\\\ (2a-5)x^2+(2-2z)x+3=0 \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \qquad \qquad \qquad \textit{discriminant of a quadratic} \\\\\\ y=\stackrel{\stackrel{a}{\downarrow }}{(2z-5)}x^2\stackrel{\stackrel{b}{\downarrow }}{+(2-2z)}x\stackrel{\stackrel{c}{\downarrow }}{+3} ~~~~~~~~ \stackrel{discriminant}{b^2-4ac}= \begin{cases} 0&\textit{one solution}\\ positive&\textit{two solutions}\\ negative&\textit{no solution} \end{cases} \\\\[-0.35em] ~\dotfill`

`(2-2z)^2~~ - ~~4(2z-5)(3)~~ = ~~0\implies (4-8z+4z^2)-(8z-20)(3)=0 \\\\\\ (4-8z+4z^2)-(24z-60)=0\implies 4z^2-32z+64=0 \\\\\\ 4(z^2-8z+16)=0\implies z^2-8z+16=0 \\\\\\ (z-4)(z-4)=0\implies \boxed{z=4}`