Question

HELP!! Due in 10 mins

Answer 1

The surface area of each half has increased by 60 cm², which is a percentage increase of 31.6% (nearest tenth).

Explanation:

The area of a rectangle is the product of its width and length.

If the object is cut in half along the blue line, each piece will increase its surface area by the area of a rectangle that is 6 cm wide and 10 cm long:

`\implies 6 \cdot 10=60\; \sf cm^2`

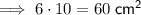
Therefore, the surface area of each piece will increase by 60 cm².

If you want to know the increase as a percentage, we first need to calculate the total surface area of the given object by summing the areas of each side.

`\begin{aligned}\implies \textsf{Total\;S.A.}&=(10\cdot 6)+(4 \cdot 6)+4(5\cdot 6)+2(3\cdot 6)+2(10\cdot 5+4 \cdot 5)\\&=60+24+4(30)+2(18)+2(50+20)\\&=60+24+120+36+2(70)\\&=60+24+120+36+140\\&=380\;\sf cm^2\end{aligned}`

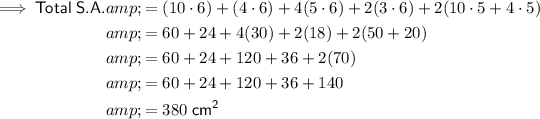
If the total surface area of the object is 380 cm², then the surface area of each half before the object was cut in half is 190 cm².

As we have already determined, the surface area of each half after the object is cut in half increases by 60 cm². Therefore, the total surface area of each piece after the object has been cut in half is:

`\implies 190 + 60 = 250 \; \sf cm^2`

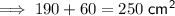
To calculate how much the surface area of each half has increased, use the percentage increase formula.

`\begin{aligned}\textsf{Percentage increase}&=\sf (final\;value-initial\;value)/(initial\;value)\\\\&=(250-190)/(190)\\\\&=0.315789...\\\\&=31.6 \%\; \sf (nearest\;tenth)\end{aligned}`

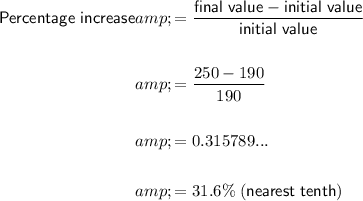
Therefore, the surface area of each half has increased by 60 cm², which is a percentage increase of 31.6% (nearest tenth).