Question

Describe the bahavior of the polynomial equation y=x^2-4

Answer 1

`\text{As x} \to \infty, \text{then } y \to \infty\\\text{As x} \to -\infty, \text{then } y \to \infty`

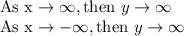
Regardless of what direction x goes to, y goes off to infinity.

In other words, it rises to the left and rises to the right

Both endpoints go up forever.

See the graph below.

====================================================

Step-by-step explanation:

As x gets bigger, x^2 gets even larger.

Examples:

• x = 100 --> x^2 = 100^2 = 10,000
• x = 1000 ---> x^2 = 1,000,000

The -4 at the end won't really put much of a dent in the large outputs as x gets really large. So we can say that as x goes to infinity, y also goes to infinity

`\text{As x} \to \infty, \text{then } y \to \infty`

Similarly,

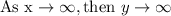
`\text{As x} \to -\infty, \text{then } y \to \infty`

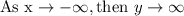
Because something like x = -100 leads to x^2 = 10,000. The negatives cancel out when squaring.

This results in both sides going up forever.

We can describe it as: It rises to the left and rises to the right.

The "rises to the left" portion is
`\text{As x} \to -\infty, \text{then } y \to \infty`

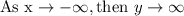
The "rises to the right" portion would be
`\text{As x} \to \infty, \text{then } y \to \infty`

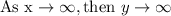
The graph is shown below. I used GeoGebra to make the graph.