Answer:
x = 15
Explanation:
Pre-Solving
We are given the following equation:
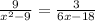
We want to find the value of x of it.
Solving
Equation
We can start by cross multiplying to get:
9(6x-18) = 3(x²-9)
Distribute the 9 and 3.
54x - 162 = 3x² - 27
Subtract 54x from both sides
-162 = 3x² - 54x - 27
Add 162 to both sides.
3x² - 54x + 135 = 0
We can divide each term by 3. We'll end up with:
x² - 18x + 45 = 0
This can be factored to become:
(x -15)(x-3) = 0
Applying zero product property,
x - 15 = 0
x = 15
And:
x-3 = 0
x = 3
Domain
We aren't done yet though; we need to find the domain of this equation, because we have variables in the denominator.
x² - 9 and 6x - 18 both cannot be zero. Because of that:
x² - 9 ≠ 0
x² ≠ 9
x ≠ ±3
and:
6x - 18 ≠ 0
6x ≠ 18
x ≠ 3
The value of x cannot be 3 or -3. This means that our only answer is x = 15.