This question is incomplete, the complete question is;
A rocket accelerates by burning its onboard fuel, so its mass decreases with time. Suppose the initial mass of the rocket at liftoff (including its fuel) is m, the fuel consumed at rate r, and the exhaust gases are ejected with constant velocity v(sub e) [relative to the rocket]. A model for the velocity of the rocket at time t is given by the equation:
v(t) = -gt - v(sub e) ln [(m-rt)/m]
where g is the acceleration due to gravity, and t is not too large. If g = 9.8 m/s^2, m = 30,000 kg, r = 160 kg/s, and v(sub e)= 3000 m/s, find the height of the rocket one minute after liftoff.
Answer:
the height of the rocket one minute after liftoff is 14.8441 km
Explanation:
Given the data in the question;
Velocity of the rocket at time t is;
v(t) = -gt -
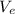 ln(
ln(
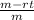 )
)
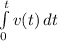 = ₀∫⁶⁰( -gt -
= ₀∫⁶⁰( -gt -
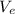 ln(
ln(
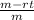 ) )dt
) )dt
= -g(
![[(t^(2) )/(2)]^(60)_0](https://img.qammunity.org/2022/formulas/mathematics/college/evid9059mfx86vvxany8x27e8nt4jd9eoj.png) -
-
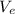 ₀∫⁶⁰In(
₀∫⁶⁰In(
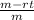 ) dt
) dt
= -g(
![[(t^(2) )/(2)]^(60)_0](https://img.qammunity.org/2022/formulas/mathematics/college/evid9059mfx86vvxany8x27e8nt4jd9eoj.png) -
-
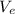 [ t In(
[ t In(
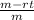 ) +
) +
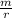 - t - mr
- t - mr
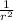 In |m-rt|
In |m-rt|
![]^(60)_0](https://img.qammunity.org/2022/formulas/mathematics/college/88ru2cudxkluj7t1q8aaugd37ynomj7s3m.png)
= -g(
![[(60^(2) )/(2)]](https://img.qammunity.org/2022/formulas/mathematics/college/rbffadziyco79hdqkd0p905f10qsfiwura.png) -
-
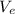 [ 60 (In(1 -
[ 60 (In(1 -
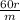 )-1) +
)-1) +
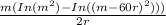 ]
]
we input our given values; g=9.8 m/s², m=30000 kg, Ve = 3000 m/s, r = 160 kg)
= -9.8(
![[(60^(2) )/(2)]](https://img.qammunity.org/2022/formulas/mathematics/college/rbffadziyco79hdqkd0p905f10qsfiwura.png) - 3000 [ 60 (In(1 -
- 3000 [ 60 (In(1 -
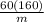 )-1) +
)-1) +
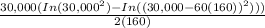 ]
]
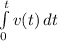 = 14844.10 m
= 14844.10 m
we convert to kilometer
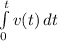 = 14844.10 ÷ 1000
= 14844.10 ÷ 1000
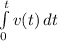 = 14.8441 km
= 14.8441 km
Therefore, the height of the rocket one minute after liftoff is 14.8441 km