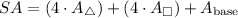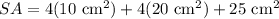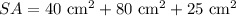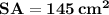Question

("Extra points")

Question: The bottom part of this block is a rectangular prism. The top part is a square pyramid. You want to cover the block entirely with paper. How much paper do you​ need? Use pencil and paper to explain your reasoning.

Answer 1

`145 \text{ cm}^2`

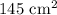
Explanation:

We can represent the surface area of the composite figure as:

`SA = 4(\text{area of triangle side}) + 4(\text{area of rectangle side}) + (\text{area of pyramid base})`

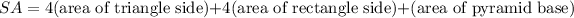
First, we can solve for the area of one of the triangle sides.

`A_\triangle = (1)/(2)bh`

`A_\triangle = (1)/(2) \cdot 5 \cdot 4`

`A_\triangle = 10 \text{ cm}^2`

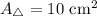
Next, we can solve for the area of one of the rectangle sides.

`A_\square = lw`

`A_\square = 5 \cdot 4`

`A_\square = 20 \text{ cm}^2`

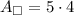
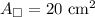
Next, we can solve for the area of the pyramid base.

`A_\text{base} = lw`

`A_\text{base} = 5 \cdot 5`

`A_\text{base} = 25 \text{ cm}^2`

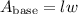
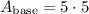
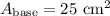
Finally, we can solve for the total surface area of the composite figure by plugging the values we just solved for into the uppermost equation.

`SA = (4 \cdot A_\triangle) + (4 \cdot A_\square) + A_\text{base}`

`SA = 4(10 \text{ cm}^2) + 4(20\text{ cm}^2) + 25\text{ cm}^2`

`SA = 40 \text{ cm}^2 + 80\text{ cm}^2 + 25\text{ cm}^2`

`\bold{SA = 145 \, \textb{ cm}^2}`