Question

Anyone please reply if you know to find x in these questions

Answer 1

b) x is about 5.4

c) x is about 21.27

Explanation:

for b), you are given the measure of two angles (the right angle measuring 90 degrees and the 78 degree angle), and the length of one side. with these values, you can use the Law of Sines to find the length of a missing side.

to make this easier lets label all sides and angles of the triangle. the right angle can be A, the 78 degree angle can be B, and the last one is C. therefor the side between angles A and B is side c, the side between angles B and C is side a, and the side between angles A and C is side b.

the Law of Sines says that if ABC has sides a,b,c then a/sinA= b/sinB= c/sinC. we can use this to find the length of side c, which is the value of X we are looking for.

first find the measure of angle C. we are given two angles in the triangle, 90 and 78, and know the total angles must measure 180 so C=180-(90+78), C=12

since we have the measure of angle A and the length of side a, I will use this to set up the equation

`\\(a)/(sinA) =(c)/(sinC) \\\\(25.9)/(sin90) =(c)/(sin12)`

solve for sin of 90 degrees and 12 degrees with calculator and then solve for c:

`(25.9)/(1) =(c)/(0.21) \\\\25.9=(c)/(0.21) \\\\c=5.44`

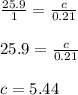
so the length of side x is about 5.4

for c), you are given the length of two sides and the included angle, so you can use the Law of Cosines to solve.

again, lets label the angles and sides to make this easier. the right angle can be A, the angle to the right of A can be B, and the bottom angle can be C. therefore the side between A and B is side C, the side between B and C is side a, and the side between A and C is side b.

according to this labeling, we are trying to find side a to solve for x.

we can use the equation

`a^(2) =b^(2) +c^(2) -2(b)(c)(cosA)`

we know side b=19.5 and side c=8.5 and angle A measures 90 degrees so fill in the values and solve for a:

`a^(2) =19.5^(2) +8.5^(2) -2(19.5)(8.5)(cos90)\\\\a^(2) =380.25 +72.25-(331.5)(0)\\\\a^(2) =452.5\\a=21.27`

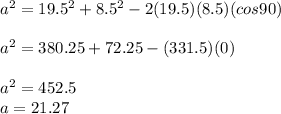
so side a is about 21.27 so that is the value of x.