Question

A-10A twin-jet close-support airplane is approximately rectangular with a wingspan (the length perpendicular to the flow direction) of 17.5 m and a chord (the length parallel to the flow direction) of 3 m. The airplane is flying at standard sea level with a velocity of 200 m/s. If the flow is considered to be completely laminar, calculate the boundary layer thickness at the trailing edge and the total skin friction drag. Assume that the wing is approximated by a flat plate. Assume incompressible flow.

Answer 1

Given :

Rectangular wingspan

Length,L = 17.5 m

Chord, c = 3 m

Free stream velocity of flow,
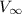`$V_(\infty)$` = 200 m/s

Given that the flow is laminar.

`$Re_L=(\rho V L)/(\mu _(\infty))$`

`$=(1.225 * 200 * 3)/(1.789 * 10^(-5))$`

`$= 4.10 * 10^7$`

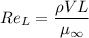
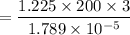
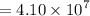
So boundary layer thickness,

`$\delta_(L) = (5.2 L)/(√(Re_L))$`

`$\delta_(L) = (5.2 * 3)/(√(4.1 * 10^7))$`

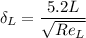
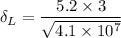
= 0.0024 m

The dynamic pressure,
`$q_(\infty) =(1)/(2) \rho V^2_(\infty)$`

`$ =(1)/(2) * 1.225 * 200^2$`

`$=2.45 * 10^4 \ N/m^2$`

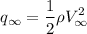
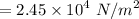
The skin friction drag co-efficient is given by

`$C_f = (1.328)/(√(Re_L))$`

`$=(1.328)/(√(4.1 * 10^7))$`

= 0.00021

`$D_(skinfriction) = (1)/(2) \rho V^2_(\infty)S C_f$`

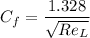
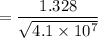
`$=(1)/(2) * 1.225 * 200^2 * 17.5 * 3 * 0.00021$`

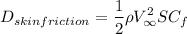
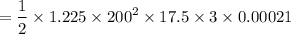
= 270 N

Therefore the net drag = 270 x 2

= 540 N