Answer:
Approximately
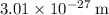 (when measured in a vacuum.)
(when measured in a vacuum.)
Step-by-step explanation:
Apply unit conversion and ensure that the mass of the baseball is in standard units (kilograms):
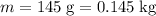 .
.
The kinetic energy of the baseball will be:
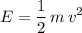 ,
,
Where
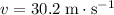 is the speed of the baseball.
is the speed of the baseball.
 .
.
The energy of a photon of frequency
 is:
is:
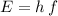 ,
,
Where
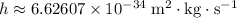 is Planck's constant.
is Planck's constant.
When measured in a vacuum where speed of light is
 , the wavelength
, the wavelength
 of this photon will be:
of this photon will be:
 .
.
 .
.
Hence, the expression for the energy of this photon can be rewritten as:
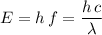 .
.
Rearrange this equation to find
 :
:
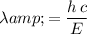 .
.
Assuming that the energy of this photon to be equal to the kinetic energy of that baseball,
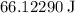 :
:
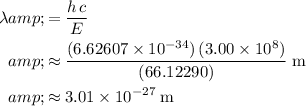 .
.