Question

6. When Frank Markenburg's social networking site went public, it was valued at

five million dollars. One year later, it was valued at 25 million dollars. If the site
was never valued below zero dollars, write the exponential function that will model
the growth of the value of the company. Use your model to find when the site will
be valued 200 million dollars.

Answer 1

• After 2.3 years

-----------------------------------

To create an exponential function we'll need to use the formula:

`V(t) = V_0 * (1 + r)^t`

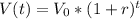
Where:
- V(t) is the value of the site at time t,
- V₆ is the initial value of the site,
- r is the growth rate,
- t is the time (in years).

Find the growth rate (r).

We know that the initial value V₆ is 5 million dollars, and the value after one year is 25 million dollars. So, we can set up equation:

• 
  `25 = 5 * (1 + r)^1`

Now, we'll solve for r:

• 5 * (1 + r) = 25
• 1 + r = 25 / 5
• 1 + r = 5
• r = 4

The growth rate (r) is 4, so the exponential function is:

`V(t) = 5 * (1 + 4)^t = 5 * 5^t`

Use this model to find when the site will be valued at 200 million dollars.

Set V(t) to 200 and solve for t:

• 
  `200 = 5 * 5^t`
• 
  `40 = 5^t`
• 
  `log_5(40) = log_5(5^t)`
• 
  `t = log_5(40)`
• t ≈ 2.292

So, the site will be valued at 200 million dollars after approximately 2.3 years.