Question

Consider the marginal cost function

C′​(x)=0.12x^2− 4x+100.
a. Find the additional cost incurred in dollars when production is increased from 2 units to 15 units.
b. If ​C(2​)=267​, determine ​C(15​) using your answer in ​(a).

Answer 1

a. To find the additional cost incurred in dollars when production is increased from 2 units to 15 units, we need to integrate the marginal cost function from 2 to 15:

`\implies\texttt\:\int_(2)^(15) C'(x) dx = \int_(2)^(15) (0.12x^2 - 4x + 100) dx`

$\texttt\:= \left[ 0.04x^3 - 2x^2 + 100x \right]_{2}^{15} \ = (0.04 \cdot 15^3 - 2 \cdot 15^2 + 100 \cdot 15) - (0.04 \cdot 2^3 - 2 \cdot 2^2 + 100 \cdot 2) \ = 1590$

Therefore, the additional cost incurred in dollars when production is increased from 2 units to 15 units is $1590.

b. We can use the information we found in part (a) and the given value of C(2) to find C(15):

`\texttt\:C(15) = C(2) + \int_(2)^(15) C'(x) dx \ = 267 + 1590 \ = 1857`

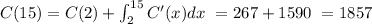
Therefore, C(15) is 1857.