Question

Geometry task!
Help please . 50 pointsss!!!!!

Answer 1

(a) Star's surface power.

(b) Star's interior power.

(c) Radius = 6 × 10¹⁰ cm

Explanation:

Since the star is a sphere, we can calculate its volume and surface area by using the following formulas:

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a sphere}\\\\$V=(4)/(3) \pi r^3$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`
`\boxed{\begin{minipage}{4 cm}\underline{Surface area of a sphere}\\\\$\vphantom{\frac12}SA=4 \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Part (a)

Given the star has a radius of about 7 × 10⁸ cm and its interior generates 3 × 10⁻⁷ watts of power per cubic centimeter, to calculate the power that the interior of the star would generate, multiply the volume of the star (in cubic centimeters) by 3 × 10⁻⁷:

`\begin{aligned} \implies \textsf{Interior power}&=V * 3 * 10^(-7)\\&=(4)/(3) \pi (7 * 10^8)^3* 3 * 10^(-7)\\&=4\pi(7^3 * 10^(24)) * 10^(-7)\\&=4\pi(343) * 10^(24) * 10^(-7)\\&=1372\pi * 10^(24-7)\\&=1372\pi * 10^(17)\\&=4310.265...* 10^(17)\\&\approx 4.31 * 10^3 * 10^(17)\\&\approx 4.31 * 10^(3+17)\\&\approx 4.31 * 10^(20)\; \sf watts\end{aligned}`

Similarly, given each square centimeter of the star's surface shines 6,000 watts of power into space, to calculate how much power the star's surface would shine into space, multiply the surface area (in square centimeters) by 6,000:

`\begin{aligned} \implies \textsf{Surface power}&=SA * 6000\\&=4 \pi (7 * 10^8)^2 * 6000\\&=4 \pi(7^2 * 10^(16)) * 6000\\&=24000 \pi(49) * 10^(16)\\&=1176000 \pi * 10^(16) \\&=1.176\pi * 10^6 * 10^(16)\\&=1.176\pi * 10^(6+16)\\&=1.176\pi * 10^(22)\\&\approx 3.69 * 10^(22)\; \sf watts\end{aligned}`

.

As the exponent on base 10 increases, the standard notation gets larger. Therefore, the power the star's surface shines into space is greater.

Part (b)

Given the star has a radius of about 5 × 10¹² cm and its interior generates 3 × 10⁻⁷ watts of power per cubic centimeter, to calculate the power that the interior of the star would generate, multiply the volume of the star (in cubic centimeters) by 3 × 10⁻⁷:

`\begin{aligned} \implies \textsf{Interior power}&=V * 3 * 10^(-7)\\&=(4)/(3) \pi (5* 10^(12))^3* 3 * 10^(-7)\\&=4\pi(5^3 * 10^(36)) * 10^(-7)\\&=4\pi(125) * 10^(36) * 10^(-7)\\&=500\pi * 10^(36-7)\\&=1570.796... * 10^(29)\\&\approx 1.57 * 10^3 * 10^(29)\\ &\approx 1.57 * 10^(3+29)\\&\approx 1.57 * 10^(32)\; \sf watts\end{aligned}`

Similarly, given each square centimeter of the star's surface shines 6,000 watts of power into space, to calculate how much power the star's surface would shine into space, multiply the surface area (in square centimeters) by 6,000:

`\begin{aligned} \implies \textsf{Surface power}&=SA * 6000\\&=4 \pi (5 * 10^(12))^2 * 6000\\&=4 \pi(5^2 * 10^(24)) * 6000\\&=4 \pi(25) * 10^(24) * 6000\\&=600000\pi * 10^(24) \\&=6\pi * 10^5* 10^(24)\\&=18.8495...* 10^(5) * 10^(24)\\ &\approx 1.88 * 10^1 * 10^5 * 10^(24)\\ &\approx 1.88 * 10^(1+5+24)\\&\approx 1.88 * 10^(30)\; \sf watts\end{aligned}`

.

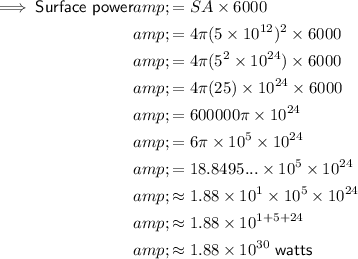
As the exponent on base 10 increases, the standard notation gets larger. Therefore, the power the star's interior generates is greater.

Part (c)

To calculate the radius of the star that makes the power generated in its interior equal to the power leaving its surface, set the volume formula multiplied by 3 × 10⁻⁷ equal to the surface area formula multiplied by 6,000 and solve for r.

`\begin{aligned}\implies \sf Power\;generated\;in\;interior&=\sf Power\;leaving\;surface\\ V * 3 * 10^(-7)&=SA * 6000\\ (4)/(3) \pi r^3 * 3 * 10^(-7)&=4 \pi r^2 * 6000\end{aligned}`

Divide both sides by 4πr²:

`\implies (1)/(3) r* 3 * 10^(-7)=6000`

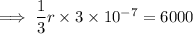
Multiply the numbers:

`\implies r * 10^(-7)=6000`

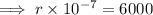
Divide both sides by 10⁻⁷:

`\implies r =(6000)/(10^(-7))`

`\implies r =6000 * 10^7`

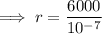
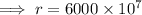
Simplify:

`\implies r =6 * 10^3 * 10^7`

`\implies r =6 * 10^(3+7)`

`\implies r =6 * 10^(10)`

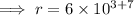
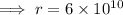
Therefore, the radius of the star for which the power leaving the surface equals the power generated in the interior is 6 × 10¹⁰ cm.