Answer:
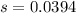
Explanation:
Given:
0.612 0.523 0.606 0.631 0.584 0.592 0.644 0.597 0.639 0.607 0.564 0.673
Required
Calculate the sample standard deviation
First, calculate the mean
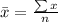
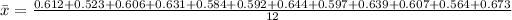
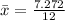
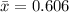
The sample standard deviation is then calculated using:
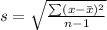
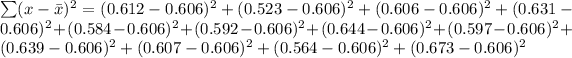
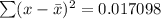
So, we have:
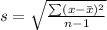


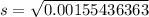
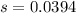 -- approximated
-- approximated