Question

Please help with calculus. Thank you.

Answer 1

`\left(4, √(13)\right)\;\textsf{and}\;\left(4, -√(13)\right)`

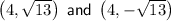
Explanation:

Let the point on the curve be (x, y).

Use the distance formula to create an equation for the distance between (8, 0) and (x, y):

`\implies d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`\implies d=√((x-8)^2+(y-0)^2)`

`\implies d=√((x-8)^2+y^2)`

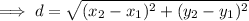
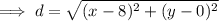
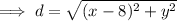
Since x² - y² = 3, then y² = x² - 3.

Substitute this into the equation so that we have an equation for d in terms of x:

`\implies d=√((x-8)^2+x^2-3)`

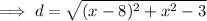
Simplify:

`\implies d=√(x^2-16x+64+x^2-3)`

`\implies d=√(2x^2-16x+61)`

`\implies d^2=2x^2-16x+61`

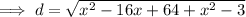
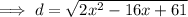
Minimize d by taking the derivative of d with respect to x::

`\implies \frac{\text{d}}{\text{d}x}d^2=\frac{\text{d}}{\text{d}x}2x^2-\frac{\text{d}}{\text{d}x}16x+\frac{\text{d}}{\text{d}x}61`

`\implies 2d\frac{\text{d}d}{\text{d}x}=4x-16`

`\implies \frac{\text{d}d}{\text{d}x}=(4x-16)/(2d)`

`\implies \frac{\text{d}d}{\text{d}x}=(2x-8)/(d)`

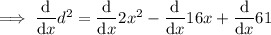
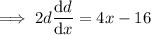
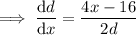
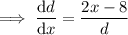
Set it to zero and solve for x:

`\implies (2x-8)/(d)=0`

`\implies 2x-8=0`

`\implies 2x=8`

`\implies x=4`

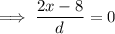
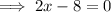
Therefore, the value of x that minimizes d is x = 4.

To find the y-coordinate(s), substitute x = 4 into the equation of the curve:

`\begin{aligned}x=4 \implies (4)^2-y^2&=3\\16-y^2&=3\\y^2&=13\\y&=\pm √(13)\end{aligned}`

Therefore, the points on the curve x² - y² = 3 that are closest to the point (8, 0) are (4, √13) and (4, -√13).