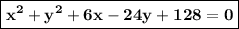you'll want to work with the center-radius form of a circle equation for this. the center formula is
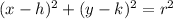 , where
, where
 is your center and r is your radius. plug in the information your circle gives you:
is your center and r is your radius. plug in the information your circle gives you:
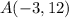 ,
,

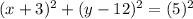 ... simplify the right side
... simplify the right side
 ... from here, you need to foil both of your binomials to convert this to the "general form" that your answer choices are in.
... from here, you need to foil both of your binomials to convert this to the "general form" that your answer choices are in.
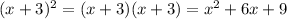

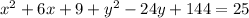 ... combine like terms
... combine like terms
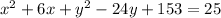 ... subtract 25
... subtract 25
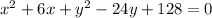 is your equation. reorder it so that it's from the highest degree to the lowest:
is your equation. reorder it so that it's from the highest degree to the lowest: