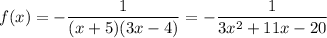Question

Hi!!! Thanks for stopping by my question! I would really appreciate the help! I've attached the question below. Thanks!

I'd appreciate if you made sure to double check your answers and provide everything the question is asking! INCLUDE ALL STEPS!

Answer 1

1. f(x) = -(x +2)(x -4)/((x +1)(x -3)); graph attached
2. f(x) = -1/(3x² +11x -20)

Explanation:

You want functions that have the given list of asymptotes and intercepts.

Asymptotes and zeros

The functions of interest here are built as rational functions of products of linear terms. Each numerator linear term (x -p) will make the function have a zero (x-intercept) of x=p. Each denominator linear term (x -p) will make the function have a vertical asymptote at x=p. The horizontal asymptote will be the value of the ratio of the leading numerator and denominator terms as x gets large in magnitude.

1. Horizontal asymptote at -1

The x-intercepts at -2 and 4 mean the numerator factors are (x +2) and (x -4).

The vertical asymptotes at -1 and 3 mean the denominator factors are (x +1) and (x -3).

In order to make the function have a horizontal asymptote of -1, the ratio of leading terms (x²/x²) must have a coefficient of -1.

One function that meets the requirements is ...

`f(x)=-((x+2)(x-4))/((x+1)(x-3))`

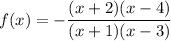
2. Reciprocal of quadratic

The vertical asymptotes at -5 and 4/3 mean the denominator factors are (x +5) and (3x -4). (We could use (x-4/3), but we prefer integers in the expression.)

The ratio of leading terms (1/x²) is positive for x not between the asymptotes, so we need a negative coefficient.

One function that meets requirements is ...

`f(x)=-(1)/((x+5)(3x-4)) = -(1)/(3x^2+11x-20)`