Question

Howdy! Thanks for stopping by my question! I would really appreciate the help! I've attached the question below. Thanks!

I'd appreciate if you made sure to double check your answers and provide everything the question is asking! INCLUDE ALL STEPS!

Answer 1

a) x = 1 ± (3/7)√7

b) (-∞, -5) ∪ [-2, 5) ∪ [6, ∞)

Explanation:

You want solutions to the relations ...

• 7 +1/x = 1/(x-2)
• (x² -4x -12)/(x² -25) ≥ 0

a) 7 + ...

We like to solve these in the form f(x) = 0. It helps avoid extraneous solutions.

`7+(1)/(x) -(1)/(x-2)=0\\\\\\(7x+1)/(x)-(1)/(x-2)=0\\\\\\((7x+1)(x-2)-x)/(x(x-2))=0\\\\\\ (7x^2-14x-2)/(x(x-2))=0`

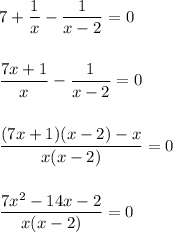
The roots of the numerator quadratic are found by ...

x² -2x -2/7 = 0 . . . . . divide by 7

x² -2x +1 -9/7 = 0 . . . . add and subtract 1

(x -1)² = 9/7 . . . . . . . . . . write as a square, add 9/7

x -1 = ±√(9·7/49) = ±(3/7)√7 . . . . take the square root

x = 1 ± (3/7)√7

b) (x² - ...

Rational inequalities are best solved by identifying the roots of numerator and denominator. These tell you where the function changes sign. The end behavior of the rational function tells you what the signs are changing from.

`(x^2-4x-12)/(x^2-25)\ge 0\\\\\\((x+2)(x-6))/((x+5)(x-5))\ge0`

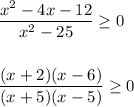
This has a horizontal asymptote at y=1 for |x|→∞. It has vertical asymptotes at x=±5.

The sign changes occur at x ∈ {-5, -2, 5, 6}. The rational expression is positive (approaching +1) for x < -5 and for x > 6. It is negative in the adjacent intervals, so positive again for -2 < x < 5.

The inequality is satisfied for ...

• x < -5
• -2 ≤ x < 5
• 6 ≤ x