Answer:
- 1/f(x) = 1/(5x² +13x -6); x = -3; x = 2/5
- graphed in the attachment. domain, increasing: (-∞, -4) ∪ (-4, 2) ∪ (2, ∞); range: (-∞, 1) ∪ (1, 1.5) ∪ (1.5, ∞); negative: (2, 5); positive: (-∞, -4) ∪ (-4, 2) ∪ (5, ∞). Not decreasing anywhere.
Explanation:
You want the reciprocal function of f(x) = 5x² +13x -6 and the equations of its vertical asymptotes. You also want the graph of f(x) = ((x +4)(x -5))/(x² +2x-8) along with its domain, range, and intervals of positive, negative, increase, and decrease.
1. f(x) = 5x² +13x -6
The reciprocal function will be ...
1/f(x) = 1/(5x² +13x -6)
Its vertical asymptotes will be found where f(x) = 0. Those values of x are nicely found by factoring the function.
f(x) = 5x² +13x -6 = (5x +15)(5x -2)/5 = (x +3)(5x -2)
The product of factors will be zero when one of the factors is zero.
x +3 = 0 ⇒ x = -3
5x -2 = 0 ⇒ x = 2/5
The equations of the vertical asymptotes are x = -3 and x = 2/5.
2. f(x) = ((x +4)( ...
The function can be simplified by factoring the denominator anc cancelling common factors:
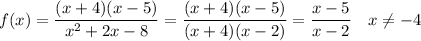
The function changes sign where the factors are zero, at x = 2 and x = 5. It is approaches the horizontal asymptote y = 1 for large positive or negative values of x, and is increasing everywhere it is defined. There is a vertical asymptote at x = 2, and a "hole" at x = -4 where the numerator and denominator factors canceled, but the function remains undefined. The function can take on any value except those at the horizontal asymptote and the "hole".
Domain, Increasing
The function is increasing everywhere it is defined, so the "increasing" intervals and the domain are the same:
(-∞, -4) ∪ (-4, 2) ∪ (2, ∞) . . . . . domain, intervals of increase
The function has no intervals of decrease.
Negative, Positive, Range
The function is positive everywhere it is defined, except for the interval between sign changes.
negative: (2, 5)
positive: (-∞, -4) ∪ (-4, 2) ∪ (5, ∞)
range: (-∞, 1) ∪ (1, 1.5) ∪ (1.5, ∞)